Measuring Outside and Inside

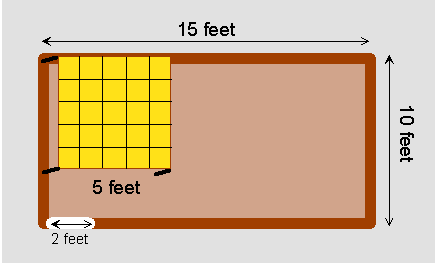
Your dad just finished building a deck out back and he wants to put a railing around it, leaving a 2-ft space as an entrance. He also needs a large piece of yellow canvas to cover a square corner of the rectangular deck, so there will be a shady spot. He asks you to help him calculate what length of railing and how much canvas to buy for the project. So you draw this diagram and insert the measures shown:

The length of the railing is 2 feet less than the perimeter or distance around the deck.
2 sides measure 10 feet, one side is 15 feet and the other is 13 feet (2 foot gap).

10 + 10 + 15 + 13 = 48 feet of railing is needed.

The yellow canvas shade cover is a square with side = 5 feet so we can " square it off " into
25 squares that measure 1 foot by 1 foot.

The area of canvas for the shade is 5 feet × 5 feet = 25 square feet (ft²).

Perimeter: Measuring Around the Outside

The prefix peri- means "around or surrounding" -- as in periscope -- the device a submarine captain uses to check what's happening at the surface, when the sub is under water. And "meter" means "measure" -- so perimeter means the measure or distance around the outside of something.

When we need to find the perimeter of an irregular figure, one with no equal sides, we just add the lengths of all the sides. If we have a square or rectangle, we can take a shortcut, because -- with a square, all sides are the same length, and with a rectangle, we've got 2 pairs of sides that are the same length. For these shapes, we develop formulas.

Because a rectangle has 2 pairs of equal sides, instead of adding their lengths separately to find perimeter, we use a formula. We can see that if we double the sum of the length and width, we'll have the perimeter. So, we "name" the length and the width l and w -- then we write the formula.

P = 2 l + 2 w = 2 ( l + w )
and for a square or a rhombus it is P = 4 s, where the length of a side = s.

The length and width of a rectangle are also called it's base and height.

Examples:

1) Find the Perimeter of:

a) A parallelogram (//gm) with top/bottom = 7 inches and sides = 9 inches
Perimeter = 2 (7 + 9) = 2 (16) = 32 inches.

b) A rectangle with length (l) = 14 ft. and width (w) = 10 ft.
Perimeter = 2 (14 + 10) = 2 (24) = 48 feet.

c) A Square with side (s) = 12 yards.
Perimeter = 4 (12) = 48 yards.

BEWARE!! of mixed units!! If one measure is inches, the other is feet, we have to convert in order to have units of the same size to add and multiply. Answers must include units!!

Example:
Find the Perimeter of a parallelogram (//gm) with top/bottom = 2 feet, side = 9 inches.
Solution: We could change feet to inches: 2 feet = 2 × 12 = 24 inches
so the Perimeter = 2 (24 + 9) = 66 inches.
Or, we could realize that 9 inches = ¾ of a foot, (¾ of 12 = 9),
so the Perimeter = 2 (2 + ¾) = 4 + 1½ = 5½ feet which also equals 66 inches.

.

Area: Covering the Surface

The things we use -- like paint, wallpaper and carpets -- to cover surfaces such as walls and floors are always measured and priced in square units. The information on every paint can label includes the number of square feet or square meters of wall space, the paint will cover.

The measure of the surface covered by a closed figure is called AREA.
We measure area in SQUARE UNITS -- square inches, square feet, square miles --
because, to measure the area of a figure, we "square it off" and then count the squares.

We see, that to completely cover the pink square ( 5 × 5 ), with grey squares ( 1 × 1 ),
we would use 5 rows of 5 squares each -- so we'd need 25 squares in all.
Area of a square that is 5 by 5 = 25 units².
Area of a square that is 9 inches per side = 81 in² (square inches).

Area Formulas
figure	Area Formula	Comments
Square	A = s²	all sides = s
Rectangle	A = l × w	length = l, width = w
Triangle	A = ½ ( b × h )	base = b, perpendicular height = h

.

Now get a pencil, an eraser and a note book, copy the questions,
do the practice exercise(s), then check your work with the solutions.
If you get stuck, review the examples in the lesson, then try again.

Practice Exercises

1) For each image in the diagram, find the perimeter, and area.
(be sure to write the formula used for both perimeter and area)

2) Draw a diagram, then solve each of these questions:
a) The Area of a rectangle = 36 in². The length l = 9 in, find the width w and Perimeter.
b) The Perimeter of a Square = 44 in. Find the length of the side s and the Area.
c) The Perimeter of a rectangle is 96 feet. If the base is twice as long as the height,
find the dimensions and the area.

3) The wooden frame around an 8 × 10 inch photo is 2 inches wide on all sides.
Find a) the perimeter of the frame; and b) the area of the wooden frame.

Solutions

1)

Perimeter	Area
a) P = sum of sides = 28.8 inches	rectangle area: A = b × h = 9 × 5 = 45 in² triangle area: A = ½ (b × h) = ½ (9 × 2) = 9 in² total area = 45 in² + 9 in² = 54 in²
b) P = 2(l + w) = 8.48 feet	A = l × w = 3.18 × 1.06 = 3.37 ft²
c) P = 4s = 28 cm	A = s² = 49 cm²
d) P = sum of sides = 29.3 yds	The figure is a 4 by 4 square and 2 triangles: square area: A = s² = 16 yd² left triangle: A = ½bh = ½ 4² = 8 yd² right triangle: A = ½bh = ½ (5.5 × 4) = 11 yd² total area = 16 yd² + 8 yd² + 11 yd² = 35 yd ²

2) a) Area = 36 in². l = 9 in, w = 36 ÷ 9 = 4 inches.

b) Perimeter = 44 in. 4s = 44 so s = 11 in. Area = 11² = 121 in²

c)

3) Since the frame is 2 inches wide all around, we add 4 inches to the dimensions of the photo.
The frame's length = 14 inches, the width = 12 inches
so P = 2(l + w) = 52 inches, and total area A = l × w = 14 × 12 = 168 in².

Area of the picture is 80 in², so the area of just the frame is 168 – 80 = 88 in².

( Plane Geometry Index )

(all content © MathRoom Learning Service; 2004 - ).