prisms: area, volume

PRISMS: SURFACE AREA AND VOLUME

3-Dimensional Solids

Three Dimensional Figures are called solids.
We measure them in three dimensions: length , width, and height or altitude.
We use linear units for the perimeter, square units to measure the surface area, and cubic units to measure the volume or capacity of the solid.

There are two kinds of 3-dimensional solids:
those based on polygons, and those based on circles.
The first category includes prisms of all shapes and pyramids.
The circular solids include cylinders, cones, and spheres.

This lesson covers surface area and volume of the polygonal solids -- prisms and pyramids.

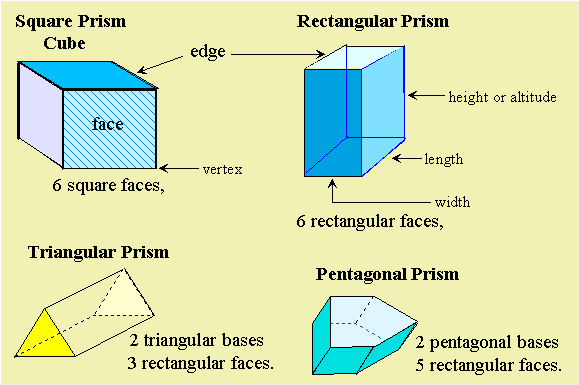
Prisms or Polygonal Solids

Prisms or Polygonal solids are composed of polygon-shaped faces, vertices or points where more than 2 sides meet , and edges, the lines where two sides meet.

A prism has 2 identical or congruent bases shaped like a polygon,
and pairs of parallel, rectangular sides.
so pyramids are not prisms.
A Prism is named for the shape of the base.

Area and Volume Formulas

Let's describe these solids and investigate the formulas for their surface area and volume.

1 Rectangular Prism: is a pile of cubes or rectangles. In common language, it's a box.
It has 6 square or rectangular faces: top and bottom, front and back, and 2 sides.

Surface Area (usually called Area) is measured in square units. It tells us how much paper or material we'd need to cover the surface of the solid.

So, The Surface Area = the sum of the areas of all the faces.

And since there are 3 pairs of congruent faces, we take 2 times the sum of the areas of 3 faces.

If as shown, the dimensions are l, w, and h for length, width and height,
the total Surface area = 2( lw + lh + wh )

Volume (also called Capacity) measured in cubic units tells us how much material a shape can hold, or how much material it contains.

Volume = Area of the base multiplied by the height so
Volume = l × w × h

2 Triangular Prism: is a pile of triangles if we stand it on end. This shape is what most people think of when they hear the word prism. It has 3 square or rectangular faces called "sides"
and 2 trangular bases.

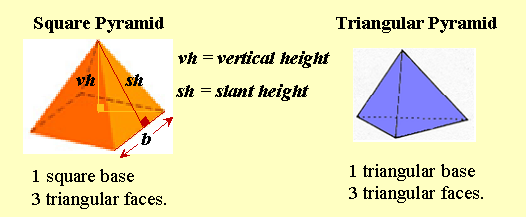
3 Pyramid: the number of sides depends on the shape of the base. It could be a square or a triangle or some other polygon. The sides or faces meet at a point called the vertex or apex.

** Warning: there are 2 different heights to consider in a pyramid: the vertical height -- from vertex to the center point of the base, and the slant height -- from vertex to the center point of a base edge. We use the slant height to find the area of the triangular sides and the vertical height to find the volume.

Surface Area = sum of the areas of the base and sides or faces.
square pyramid: area of the square base plus the areas of the 4 triangular sides.
triangular pyramid: areas of the 4 triangles -- the base and 3 sides.

Volume = (Area of base × height).

Note:
for straight sided solids (prisms, cylinders): Volume = (area of base) × height
for pointy slanted sided solids (pyramids, cones): Volume = (area of base × height).

Now get a pencil, an eraser and a note book, copy the questions,
do the practice exercise(s), then check your work with the solutions.
If you get stuck, review the examples in the lesson, then try again.

Practice Exercise

Remember to include the proper units in your answers.

Reminder: the area of a triangle is ½ base × height.

1) For each figure shown:

a) name the figure .......... b) find the total surface area .......... c) find the volume.

Solutions

1) a) rectangular prism .......... cube (square prism) .......... triangular prism.

b) rectangular prism: Area = 2(4 × 9 + 4 × 6 + 6 × 9) = 228 cm²
cube (square prism): Area = 6(16²) = 1536 mm²
triangular prism: Area = 2(3 × 5) + 3(11 × 5.8) = 221.4 cm².

c) rectangular prism: Volume = 4 × 6 × 9 = 324 cm³
cube (square prism): Volume = 16³ = 4096 mm³
triangular prism: Volume = 3 × 5 × 11 = 165 cm³.

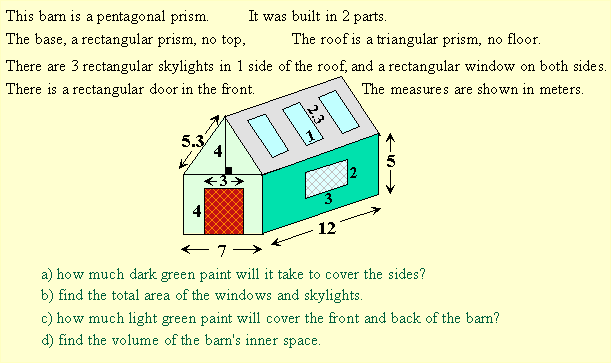
a) each side is 12 × 5 = 60 m² less the 6 m² for the window.
Total dark green paint area = 2(60 – 6) = 108 m².

b) The windows are each 6 m² and each skylight is 2.3 m²
total area of windows and skylights is 2(6) + 3(2.3) = 18.9 m².

c) the back of the barn is a rectangle (7 × 5) and a triangle (b = 7, h = 4)
Area of the back of the barn is 35 + 14 = 49 m².
The front of the barn is 12 m² less because of the door, so
total area of light green paint to cover the front and back = 49 + 49 – 12 = 86 m².

d) the volume of the rectangular prism is 7 × 12 × 5 = 220 m³
the volume of the triangular prism is ½ (7 × 4 × 12) = 168 m³
total volume of the inner barn space is 220 + 168 = 388 m³

( Plane Geometry MathRoom Index )