| Vectors |
.
Note: vectors are always displayed in vertical form in these lessons to differentiate them from points. Vectors are bold text (u), scalars are italics (k).
Definition: A scalar or constant is a physical quantity that indicates only magnitude
Definition: A vector is a physical quantity that indicates both magnitude and direction.
Think of a wind speed -- say South -West at 20 kilometers/ hour. The 20 km/h is the magnitude, and South-West is the direction.
Definition: A zero vector denoted 0 has no magnitude. It is the additive identity:
ie u + 0 = 0 + u = u
(It goes nowhere in every direction.)
Vectors are classified by dimension: the number of components in the vector or coordinates in the initial and terminal points.
We say that u is in R² (the 2-dimensional REAL numbers) and
v is in R³ (the 3-dimensional REAL numbers)
A vector with n components or entries is called an n-dimensional vector.
Any vector of dimension > 3 is abstract so we use an algebraic
rather than geometric approach.
Vectors of the same dimension can be combined algebraically.
Two vectors are equivalent (equal) if and only if their
dimensions and components are identical.
.
All properties defined here on vectors in R³ apply to vectors in any dimension.
 |
 |
k is a scalar or constant |
u + v =  |
u – v =  |
ku =  |
.
The norm or length (magnitude) of a vector is found using the Pythagorean Theorem.
Notation: || u || denotes the norm of vector u
If u is a 3-dimensional vector, 
Also, if P1 ( x1 , y1, z1 ) and P2 ( x2 , y2 , z2 ) are the intial and terminal points of a vector, then:
.
Unit Vector: a vector of the form 
has norm = 1. It is a unit vector.
Example 1
Given that 
| a) 2u – v | b) – 3u + 5v | c) – w – 2x | d) 5w – x | |
 |
 |
 |
 | |
| e) || u || | f) || w || | g) || ½ x || | ||
 |
 |
 |
||
.
Vector Between 2 Points
Since vectors have direction, there is an initial point -- where it starts,
and a terminal point -- where it ends. The arrow is on the terminal point.
If P1 (x1, y1, z1), and P2 (x2, y2, z2) are the initial and terminal points of a vector then:
vector P1P2 = 
For vectors such as u = 
, the intial point is the origin.
So the coordinates of the terminal point P2 ( u1 , u2 , u3 )
are the same as the components of u.
To find the vector sum (u + v) geometrically, use the Parallelogram Law which states:
The sum of vectors u and v is the diagonal vector
of the parallelogram formed by u and v. (see diagram)
For u – v find u + ( – v ).
A scalar multiple of any vector kv is parallel to v
The norm of a scalar multiple vector equals the absolute value of the scalar
times the norm of vector v
|| kv || = | k | · || v ||
.
Note: you may see "h" instead of 
in the equations of this section since we don't all have the same fonts. Change cos h to 
and you'll be all right.
definition: The dot product u $ v = É u É É v É cos h
where h is the angle between u and v. The dot product of two vectors is a scalar
u $ v = u 1 v1 + u 2 v 2 + u 3 v3
Properties of the Dot Product
The sign ( + or – ) of the dot product tells us the size of the angle between u and v.
Since É u É É v É cos h is the product of 2 vector norms (positive values) and the cosine of the angle between those vectors, the sign of the dot product is the same as the sign of cos h.
So, if the dot product is negative, we know h must be in the 2nd quadrant which means it is obtuse ( > 90° ). Since cos 90° = 0, if u $ v = 0, the vectors are perpendicular or orthogonal to each other.
| if u $ v > 0 then h < 90° | if u $ v < 0 then h > 90° | if u $ v = 0 then h = 90° |
| To prove two vectors are orthogonal, show that their dot product = 0. |
(For a full explanation of the geometric and algebraic definition of the dot product, click here.)
Example 2
Determine the type of angle -- acute, obtuse or right -- between u and v.
Solution
| a) u $ v = 0, right angle. | b) u $ v < 0, obtuse angle. | c) u $ v > 0, acute angle. |
.
.
w1 = proj v u =  |
w2 = u - w1 |
so, w1 = kv or the vector component of u along v,
and w2 = u - w1 or the vector component of u orthogonal to v.
(see Orthogonal Projections lesson in this MathRoom)
Distance From a Point to a Line
the formula for the shortest distance from point P(x0, y0) to line ax + by + c = 0 is
It is based on the formula for the norm of vector w2 -- which is the distance we want.
The only difference here is that instead of the vector components,
we have the equation of the vector as a line. Learn the formula and use it.
The cross product of 2 vectors is a vector that is perpendicular or orthogonal to both original vectors so it only exists in R3.
To find u % v, set up the matrix 
, and express the determinant.
,
This vector expressed as ai + bj + ck is u % v.
Example 3
Find u % v if 
Solution
If we find u $ (u % v), it will = 0. Same for v $ (u % v).
The cross product u % v is orthogonal to both u and v.
Properties of the Cross Product
if u, v, and w are vectors in R3 and k is any scalar, then:
| a) u % v = -(v % u) | b) u % (v + w) = (u % v) + (u % w) |
| c) (u + v) % w = (u % w) + (v % w) | d) k(u % v) = (ku) % v = u % (kv) |
| e) u % 0 = 0 % u = 0 | f) u % u = 0. |
| g) || u % v || = || u || || v || sin h |
Area and Volume from Cross Product
The area of the parallelogram formed by u and v is || u % v ||.
So ½ || u % v || = the Area of the triangle defined by u and v.
The scalar triple product is defined as u $ (v % w) = 
is the volume of the parallelapiped (3-dimensional parallelogram)
formed by vectors u, v and w if they're not in the same plane.
If any 2 of the vectors are in the same plane u $ (v % w) = 0.
This is the way to prove 2 vectors are in the same plane.
.
Example 4
Prove that u, v and w are coplanar.
Solution
We must show that the scalar triple product equals zero.
so u $ (v % w) = 0
Therefore, u, v and w are in the same plane.
.
The dot product of 2 vectors is defined as || u || || v || cos h .
From the diagram, we see that w = v - u, and from
the Law of Cosines: || w ||² = || u ||² + || v ||² - 2|| u || || v || cos h
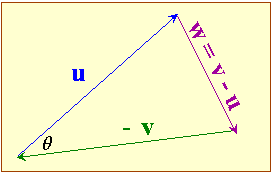
But, w = v - u so we have || (v - u) ||² = || u ||² + || v ||² - 2|| u || || v || cos h
Therefore, || u || || v || cos h = ½ (|| u ||² + || v ||² - || (v - u) ||²)
|| u || || v || cos h = ½ ( u1² + u2² + u3 ² + v1² + v2² + v3 ² - [(v1 - u1)² + (v2 - u2)² + (v3 - u3)²])
Which works out to be u1 v1 + u 2 v 2 + u 3 v3
.
Notice how we use geometry, algebra and trig in unison to approach the problem.
.
For practice on these topics do in assignment 3 questions 1 - 10.
.
back to Linear Algebra MathRoom Index
.
.
(all content © MathRoom Learning Service; 2004 - ).