
| LINEAR ALGEBRA NOTES Determinants, Cramer's Rule |
Determinants
There is a function defined only on SQUARE matrices known as the determinant.
It is denoted det(A), and is a Real number.
It is found through multiplication and addition of the matrix entries.
Determinant of a 2 × 2 Matrix
det(A2 x 2) = product of main diagonal minus product of minor diagonal.

Note: det A is indicated by a matrix with straight line sides (not brackets [ ] )
Example 1

.
Determinant of a 3 × 3 Matrix
To find the determinant of a 3 × 3 Matrix, we break it down into
three 2 × 2 determinants, each of which is multiplied by an entry from A.
we can expand by any row or any column.
We choose an entry
if the sum of its subscripts is even -- we don't change the sign
if the sum of its subscripts is odd -- we change the sign.
multiply the entry we choose by the determinant of the 2 × 2
left after we eliminate the column and row of the chosen entry.
We expand by an entire row or column and sum the results. Like this;
Example 2

We expanded the determinant by the first row.
Since a11 = 1 and 1 + 1 = 2 is even, we don't change the sign of the entry.
However, in the 2nd step, we put negative before the 7 because the entry is a12
so the sum of the subscripts is odd (1 + 2 = 3), we change the sign.
In the 3rd step, the entry is a13 so we don't change the sign.
Let's do it again but this time we'll expand by the 3rd row.

Note: look for rows or columns with 1's and 0's. It makes things easy.
.

Determinant Theorems
1) if A has a row or column of zeros, det(A) = 0
2) The determinant of a triangular matrix = the product of the entries on the main diagonal.
3) If a row of A is multiplied by a non-zero constant k, then det(A) is also multiplied by k.
4) If 2 rows of A are interchanged, det(A) is multiplied by – 1.
5) If 2 rows or 2 columns of A are proportional, det(A) = 0
6) Combining 2 rows of A has no effect on det(A).
7) If A and B are square matrices of the same size, then det(AB) = det(A)det(B).
8) A-1 exists if and only if det(A) g 0
9) det(A-1) = 1/det(A).
10) det(A) = det(At).
Example 3

a) det = – 3 -- we combine 2 rows, so no change
b) det = – 9 -- we multiply row 2 by 3 so we multiply determinant by 3
c) det = + 3 -- we switch 2 rows -- that multiplies determinant by – 1
d) det = 0 -- 2 rows are proportional.
.
Cramer's Rule
If A is an invertible square matrix, then the system AX = B has a unique solution.

where A1 is the matrix A with its 1st column replaced by the constant column etc.
Example 4
Solve the system using Cramer's rule.
We set up the 3 matrices A, A1 and A2 to find their determinants.
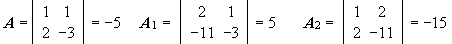
The solution is: x = 5/ – 5 = – 1 and y = – 15/ – 5 = 3
Example 5
Use Cramer's rule to solve the system

We set up the 4 matrices A, A1 , A2 and A3 to find their determinants.


.
Practice
1) Find each determinant twice. First, expand by a row, second by a column.

2) Given that  find:
find:

3) Use Cramer's rule to solve the system

.
![]()
Solutions
1) det(A) = 30. Expand by the 2nd row (it has 2 zeros) and the 1st column.
det(B) = 5. Expand by the 1st row and the 1st column.
.
2)
| a) det = –36 | b) det = – 6 | c) det = – 6 |
3)
| det (A) = –132 | det (A1) = –36 x = 3/11 |
det (A2) = –24 y = 2/11 |
det (A3) = 12 z = –1/11 |
.
(all content © MathRoom Learning Service; 2004 - ).