| DIVISION PRIMER |
What is Division?
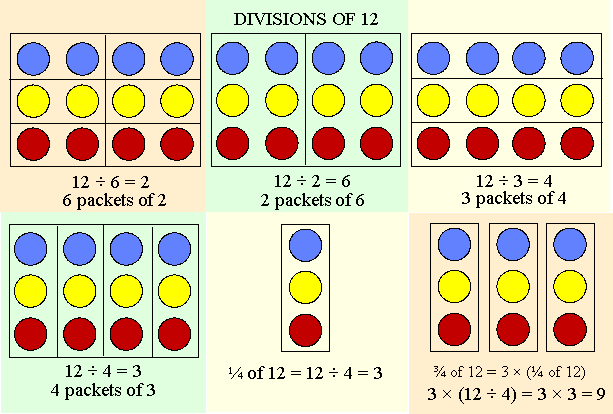
Multiplication is repeated addition. Division is the inverse operation (opposite action) of multiplication, so -- division is repeated subtraction. If 4 of us share the cost of a $12 pizza, we each pay $3 because 4 × 3 = 12, therefore 12 ÷ 4 = 3. This means we could separate $12 into 4 "equal packets" of $3 each.
12 - 3 - 3 - 3 - 3 = 0
But since division is the inverse operation of multiplication, and repeated subtraction could become extremely time consuming once the numbers are big -- we use the multiplication tables, combined with our knowledge of factors and estimating, to help us divide numbers efficiently.
Fractions mean division. When we take ½ of anything, we divide it by 2. When we find ¼, we divide by 4. And, since ¾ is the same as 3 × ¼ , when we take ¾ of something, we divide it by 4 and multiply it by 3.

Division Vocabulary
Since math is a language, we have to pay special attention to the words we use to name the different numbers and symbols in our work. We use 3 terms -- multiplier, multiplicand and product -- to name the parts of a multiplication expression. We use 4 terms to name the parts of a division expression.
The dividend is the number to be divided. If the division is presented as a fraction, it is the numerator. The number doing the dividing is called the divisor, or the denominator (in the fraction). The result or answer is called the quotient. At times, there is a remainder -- which, like its name says -- is left over once we subtract all the whole-number "divisor-sized packets" we can, from the dividend. When we divide an odd number by an even one, there will always be a remainder of 1, since any odd number is 1 bigger than the preceding even number.
Say 3 of us want to share 7 candy bars equally. After each of us takes 2 whole candy bars, there will be one left over. That's why it's called the remainder. We each get one third of that last remaining bar, so a fair share of 7 candy bars for 3 people is 2 and a third bars each.
If our pizza had cost $13 instead of $12, an equal share of the cost would be 13 ÷ 4 = 3¼ or 3.25. Once we each pay $3, there will be $1-more left to pay. So, each of us contributes another $¼ or 25¢, and the 13th dollar is paid.
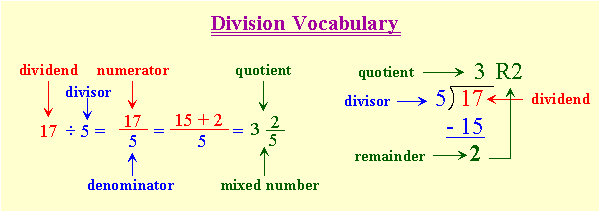
In the 2nd fraction above -- the one with 15 + 2 in the numerator.
We rewrote or regrouped 17 as 15 + 2 because 15 = 5 × 3 -- a multiple of 5 and therefore divisible by 5 -- and since we're trying to divide by 5 -- that's a good thing!! 15 is also the greatest whole number multiple of 5 that we can subtract from 17 -- and that's what we want. When we divide 15 by 5, we get 3 -- the whole number part of the quotient. We have a remainder of 2 that needs to be divided by 5 -- so our answer is  . Notice the remainder of 2 on the right side.
. Notice the remainder of 2 on the right side.
If 5 of us shared a cab that cost $17, we'd each have to contribute $3.40
because two-fifths of a dollar = 40¢.
what to do with the remainder?
There are 2 ways to deal with the remainder. Either we express the quotient as a mixed number with fraction part made up of the remainder over the divisor, or we write " R " and the remainder value next to the quotient -- shown above in the example on the right.
.
Examples with no Remainder:
Here is the 7 times table. It lists multiples of 7 from 7 × 1 to 7 × 9.
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 |
It tells us that 14 ÷ 7 = 2, and 42 ÷ 7 = 6 and so on.
If we divide any number in the 2nd row by 7 we will get a whole number quotient = to the number in the 1st row. So when we divide a multiple of 7 by 7, there will be no remainder.

Examples with Remainders:
When we divide a number that is not a multiple of 7 by 7, there will be a remainder.

Checking our Division
When we do math questions, we must always check our work, because mathland is a perfect place where coming close is no good at all. When we do math, we aim for perfection.
To check a division question:
multiply quotient × divisor then add the remainder.
In the examples above:
| (5 × 7) + 4 = 39, | (3 × 7) + 2 = 23 | (7 × 7) + 5 = 54 |
Summary of Steps in Division
1. For single-digit divisors, divide, multiply and subtract.
2. Express remainders as fractions or with uppercase " R " and the remainder's value.
4. To check, multiply quotient by divisor, add the remainder, get the dividend.
Now get a pencil, an eraser and a note book, copy the questions,
do the practice exercise(s), then check your work with the solutions.
If you get stuck, review the examples in the lesson, then try again.
![]()
.
Practice Exercises
1) Use the multiplication tables to find these quotients.
| a) 56 ÷ 8 = | b) 25 ÷ 5 = | c) 45 ÷ 9 = | d) 32 ÷ 4 = |
| e) 63 ÷ 7 = | f) 24 ÷ 3 = | g) 48 ÷ 6 = | h) 81 ÷ 9 = |
2) Find these quotients and remainders.
| a) 59 ÷ 8 = | b) 26 ÷ 5 = | c) 47 ÷ 9 = | d) 35 ÷ 4 = |
| e) 69 ÷ 7 = | f) 23 ÷ 3 = | g) 51 ÷ 6 = | h) 88 ÷ 9 = |
3) Shawna, Jennifer, Tanya and Sofia shared a taxi when they went to the museum. The meter said $12.50 and they wanted to tip the driver $1.50. What was each girl's share of the taxi fare?
![]()
.
Solutions
1) Use the multiplication tables to find these quotients.
| a) 56 ÷ 8 = 7 | b) 25 ÷ 5 = 5 | c) 45 ÷ 9 = 5 | d) 32 ÷ 4 = 8 |
| e) 63 ÷ 7 = 9 | f) 24 ÷ 3 = 8 | g) 48 ÷ 6 = 8 | h) 81 ÷ 9 = 9 |
2) Find these quotients and remainders.
| a) 59 ÷ 8 = 7 R3 | b) 26 ÷ 5 = 5 R1 | c) 47 ÷ 9 = 5 R2 | d) 35 ÷ 4 = 8 R3 |
| e) 69 ÷ 7 = 9 R6 | f) 23 ÷ 3 = 7 R2 | g) 51 ÷ 6 = 8 R3 | h) 88 ÷ 9 = 9 R7 |
3) The meter plus the tip = $14, then we ÷ 4 to get 3 R2 -- and since 2/4 = ½,
each girl's share of the taxi fare is $3.50.
![]()
( freebies index )