
| Analytic Geometry: Points & Distances |
ANALYTIC GEOMETRY
In Euclidean or Plane Geometry, when we prove geometric theorems or deductions, we do not use algebraic techniques with the geometry. With analytic or coordinate geometry -- we use both algebra and geometry cooperatively, sort of like the audio and video components of television combine to create a unified presentation. Algebra is the language or audio portion of the show and geometry is the video portion. In analytic geometry, the equation of a curve is a name or address for that curve.
Analytic Geometry was first developed around 1637 by René Descartes, a French mathematician. He developed this branch of mathematics in order to solve geometric problems by algebraic methods and gave us the means to develop problem solving methods which simplify many branches of science such as engineering and rocketry. His name -- René Descartes -- means "reborn of the maps" since in French, René means "reborn" and des cartes means "of the maps". And what did this wonderful man do? He gave us the ability to map every point in the universe by using 2 or 3 coordinates to define its position -- that's what he did. And through his work, mathematics was "reborn". Quite appropriate for a man named René Descartes, n'est-ce-pas?
It was analytic or coordinate geometry which enabled scientists to figure out the correct curvature for the mirror in the Hubble Space Telescope and with it, engineers construct the precise banking angles for the highway curves on which we travel. It is analytic geometry which enables us to make city street maps and to create images from pixels on a monitor screen so's Dad can get his dose of Pac Man or Myst. Without the work of René Descartes we would be in the dark ages mathematically -- and our sciences would be far from developed.
The Cartesian Plane
What René Descartes did to create coordinate geometry was to apply axes to the plane and three dimensional space so that every point had an address or a set of coordinates which defined that point exclusively. This is why we refer to the Cartesian plane and Cartesian coordinates. In this lesson, we will work exclusively with the two dimensional plane (R2) and leave the three dimensional work for later courses such as calculus and linear algebra. We'll see that now, when we speak of a triangle, a line or an angle, we can specify exactly where that triangle, line or angle is located and we can find values for lengths and areas quite easily.
The Coordinate Axes, Quadrants and Points
The coordinate axes are two straight lines marked off in units, which we use as references to identify the points in the plane. The X-axis is a horizontal line that measures movement left and right while the Y-axis is a vertical line which measures movement up and down.
As you can see in the diagram, the axes divide the plane into four quadrants or areas.

The axes meet at point O called the origin. The portion of the x-axis which lies to the right of the origin is the positive x-axis and the portion to the left is the negative x-axis. Notice in the diagram, the positive and negative numbers on the x-axis correspond to the right and left sides. Similarly, on the y-axis, the numbers above the origin are positive and those below the origin are negative.
So, in Quadrant I, both the x and y values of all points are positive.
In Quadrant II, the x values are negative while the y values are still positive.
In Quadrant III, both the x and y values of all points are negative.
In Quadrant IV, the x values are positive but the y values are negative.
The coordinates of a point are stated as an ordered pair.
The order is always x value first and then y value.
The correct way to write the coordinates of a point is (x, y), so the points P, R and S in the diagram have the coordinates shown. The origin is at (0, 0).
.
Definitions:
Points on the Axes:
1) Any point on the x-axis has a y-value of 0. So any point on the x-axis has coordinates (x, 0).
2) Any point on the y-axis has an x-value of 0. So any point on the y-axis has coordinates (0, y).
The Midpoint of a Line Segment
When we know the coordinates of the end points of a line segment, and we want to know the coordinates of the midpoint, we average the x values and the y values. In other words, we add the two x values and take half of the sum to get the x coordinate of the midpoint, then we add the two y values and take half of that sum to get the y coordinate of the midpoint.
| The coordinates of the midpoint of a line segment with end point coordinates (x0, y0) and (x1, y1) are  , ,which is the average of the endpoint coordinates. |
To find a mid-point, average the coordinates. After all, you know the middle is the mean or average and you learned how to find an average in grade 6. So don't bother learning another formula -- learn the technique instead -- average the coordinates!!!
The Length of a Line Segment
When we know the coordinates of the end points of a line segment, and we wish to know the length of that line segment, we use a technique based on Pythagoras' Theorem as shown in the diagram.
We are given two points, A and B with coordinates (5, 2) and (-3, -4) respectively. When we create the right triangle ABP, we can see that the length of BP is equal to the difference between the x values and the length of AP equals the difference between the y values. Now, applying the Pythagorean Theorem, we see that the length of AB is equal to the square root of the sum of the squares of the lengths of AP and AB.
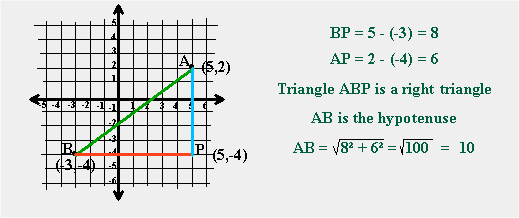
| The distance between the points (x0, y0) and (x1, y1) is equal to  |
This is known as the distance formula.
Example: Find
(a) the midpoint coordinates
(b) the length of the line segment with end points A(-3, 5) and B (17, 21).
Solution
(a) The coordinates of the midpoint of AB are 
(b) The length of line segment AB is 
![]()
.
Now get a pencil, an eraser and a note book, copy the questions,
do the practice exercise(s), then check your work with the solutions.
If you get stuck, review the examples in the lesson, then try again.
![]()
Practice
1) Plot these points on a Cartesian plane and state in which quadrant they are:
| a) A(-3, 2) | b) B(4, 7) | c) C(-2, -5) | d) D(3, -6) |
2) Find the midpoints of AB, BC, CD and AD in question 1.
3) Find the lengths of the line segments AC, BD, AD in question 1.
4)

Triangle ABC has vertices at A(2, 7) B (0, 0) and C(5, 1)
![]()
.
1) Plot these points on a Cartesian plane and state in which quadrant they are:

2) Find the midpoints of AB, BC, CD and AD in question 1.
midpt. of AB = 
midpt. of BC = (1, 1)
midpt. of CD = ![]()
midpt. of AD = (0, -2)
3) Find the lengths of the line segments AC, BD, AD in question 1.
A=(-3, 2), C=(-2, -5): length AC = 
B=(4, 7), D =(3, -6): length BD = ![]()
A=(-3, 2), D =(3, -6): length AD =![]()
4)

Triangle ABC has vertices at A(2, 7) B (0, 0) and C(5, 1)


( Freebies Index )