0 is a quadratic function.
| Quadratic Function |
A function of the form f (x) = ax2 + bx + c; a 0 is a quadratic function.
This is the General Form of the function rule.
If we graph this relationship on a Cartesian plane, we get a parabola.
In order to make the graphing easier, let's find a way to determine the vertex and axis of symmetry or fold line of the curve.
First, we put the function rule into Standard Form
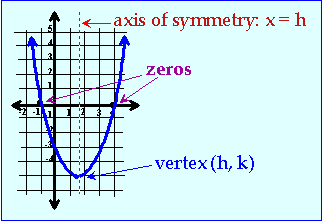
f (x) = a(x – h)2 + k.
The values for parameters a, h and k tell us what we need to know to graph efficiently.
| The graph of f (x) = a(x – h)2 + k is a parabola which: i) opens upwards if a > 0 and downwards if a < 0 ii) has vertex at (h, k) iii) the line x = h is the axis of symmetry iv) has a minimum if a > 0 and a maximum if a < 0 |
In order to put f (x) = ax2 + bx + c into Standard or Function Form, we could use the technique of completing the square (see Algebra lesson 6.2) if we were feeling masochistic.
However there is a kinder, gentler way.
Let's do an example both ways so you have a choice. I highly reccomend the 2nd method.
Example 1
Use completing the square to put f (x) = x2 – 6x + 4 into Standard Form.
Solution:
f (x) = x2 – 6x + 4 
f (x) = (x2 – 6x + 9 – 9) + 4 
f (x ) = (x – 3)2 – 5
So a = 1, h = 3 and k = – 5
The vertex is (3, – 5), the axis of symmetry is the line x = 3 and y = – 5 is a minimum value.
Note: Since the axis of symmetry is a line, we must write an equation of the line!
We can't just say the axis of symmetry is 3. This would mean that the axis of symmetry is just a point on the number line rather than an infinite set of points -- a line.
This example is simple since the coefficient of x2 , a = 1. However, things get a little more complicated when a is not = 1. The most common mistake we make when we complete the square, is to forget to multiply by a, the constant term that we add to the expression,.
Since none of you understand a word I just said -- you'll believe me when I say there's a simpler, more efficient, less painful way to do this.
So, now let's do it efficiently -- the sane man's way:
.
|quadratic function | general to standard form | x and y intercepts |
graphing from standard form | another approach to graphing | practice | solutions
Changing from General to Standard Form:
| Start with: f (x ) = ax2 + bx + c, | End with: f (x) = a(x – h)2 + k |
h, the x-value of the vertex is found with 
,
k, the y-value of the vertex = f (h).
, k = f (h),
so f (x) = ax2 + bx + c becomes 
f (x) = x2 – 6x + 4, which means that a = 1, b = – 6, and c = 4
, and k = f (3) = – 5
f (x) = (x – 3) 2 – 5.
Example 2: Find the vertex of the parabola f (x) = – 2x2 + 8x – 7.
Write the rule in standard form.
a = – 2, b = 8 and c = – 7
, so f (2) = 1, and the vertex is at (2, 1)
The standard form of this function rule is f (x) = – 2(x – 2)2 + 1
Since a < 0, the curve opens downward thus y has a maximum value of 1.
Note: the first parameter "a" is the same in all 3 forms of the quadratic function rule. The third form of the rule is the Zeros Form and indicates the x-intercepts of the curve.
It is of the form f (x) = a ( x – x 1 )( x – x 2 )
where x 1 and x 2 are the zeros or x-intercepts.
.
Example 3
Put these quadratic functions into standard form.
State the vertex, equation of the axis of symmetry and maximum or minimum value.
| (a) f (x) = 3x2 + 24x + 10 | (b) y = 2x2 + 12x – 1 | (c) y = – 2x2 + 10x – 7 |
Solutions:
(a) f (x) = 3x2 + 24x + 10 
a = 3, b = 24, and c = 10
so h = 
, k = f (h) = 3( – 4)2 + 24( – 4) + 10 = – 38
so the final form is f (x) = 3(x + 4)2 – 38
Since x + 4 = x – ( – 4) , the vertex is ( – 4, – 38), the axis of symmetry is x = – 4 and, since
a = 3 > 0, the curve opens upwards so f (x) = – 38 is a minimum value for f (x).
(b) f (x) = 2x2 + 12x – 1 
a = 2, b = 12, and c = – 1
so h = 
, k = f (h) = 2( – 3)2 + 12( – 3) – 1 = – 19
so the final form is f (x) = 2(x + 3)2 – 19
Since x + 3 = x – ( – 3), the vertex is ( – 3, – 19), the axis of symmetry is x = – 3 and, since
a = 2 > 0, the curve opens upwards so f (x) = – 19 is a minimum value for f (x).
(c) f (x) = – 2x2 + 10x – 7 
a = – 2, b = 10, and c = – 7
so h = 
, and k = f (h) =
so the final form is 
The vertex is 
, the axis of symmetry is 
and,
since a = – 2 < 0, the curve opens downwards so f (x) = 
is a maximum value for y.
.
|quadratic function | general to standard form | x and y intercepts |
graphing from standard form | another approach to graphing | practice | solutions
.
Just as with lines, finding the x and y intercepts of a parabola can help us draw the graph of the curve. Parabolas which are symmetric to a line parallel to the y-axis always have a y-intercept which, as always, is found by setting x = 0.
The y-intercept of such a parabola in General Form = c, since, when we set x = 0, the x2 and x terms disappear leaving only the constant term c = y.
For example, in f (x) = – 2x2 + 10x – 7, if we set x = 0, we get y = – 7.
| The y-intercept of f (x) = ax2 + bx + c is (0, c). |
There are three possibilities for the x intercepts of a parabola with axis of symmetry parallel to the y-axis. The diagram shows us there can be 2, 1 or 0 x-intercepts.
So how do we tell from the function rule whether the parabola has 0, 1 or 2 x-intercepts or zeros? In exactly the same way we figured out whether a quadratic has 0, 1 or 2 solutions.
We set f (x) = 0 and if the trinomial doesn't factor, we look at the discriminant.
Recall that if the discriminant b² – 4ac is negative (< 0), there are no real roots,
if it equals 0, there is a unique root or two equal roots, and
if the discriminant is positive, there are two unequal or distinct roots.
If the trinomial factors, we can easily see if there is one root or two when we set
f (x) = 0, since a trinomial that factors always has roots.
If we get a perfect square, there is only one real root or two equal roots.
If the trinomial factors as the product of two different binomials, there are two roots.
Here are some examples.
Example 4
Find the x intercepts for
| (a) y = x2 + 6x + 9 | (b) y = x2 + 6x + 5 | (c) y = x2 + x + 5 |
Solutions:
(a) 0 = (x + 3)2 
x = – 3 (2 equal roots)
(b) f (x) = (x + 1)(x + 5) 
x = – 1 or x = – 5
(c) discriminant = – 19 so there are no real roots.
.
|quadratic function | general to standard form | x and y intercepts |
graphing from standard form | another approach to graphing | practice | solutions
.
In order to graph the parabola defined by f (x) = a(x – h)2 + k , it is best to locate the vertex, the axis of symmetry and at least one pair of partner points on either side of the axis of symmetry. By partner points, we mean two points with the same y-value. In many cases, it is recommended that we find two pairs of partner points, well separated from each other, in order to have a good indication of the shape of the parabola. We could of course just make a table of x and y values, but that is not the most efficient way of doing things, and in math, efficiency is always an objective, so let's look at the process of graphing f (x) = – 2x2 + 10x – 7 efficiently.
First, we complete the square to put the equation in standard form: 
Now, we plot the axis of symmetry x = 5/2 and the vertex 
as seen in diagram A.
We then substitute two values for x which are symmetric about the axis of symmetry, into the equation for f (x). We will use x = 1 and x = 4. We find f (x) = 1 for both, so we add the points (1, 1) and (4, 1) to our graph, (diagram B) and now, just to make sure, we graph the y intercept (0, – 7) and its partner point (5, – 7) (diagram B). Now we can join the points to finish graphing the parabola (diagram C) with:
vertex at
, axis of symmetry is the line x = 5/2, y has a maximum value of 11/2.
.
|quadratic function | general to standard form | x and y intercepts |
graphing from standard form | another approach to graphing | practice | solutions
Another Approach to Graphing f (x) = ax2 + bx + c
There is another way to graph the quadratic function f (x) = ax2 + bx + c if the trinomial can be factored. Since we know that the axis of symmetry is always half way between any pair of partner points, and we know that the vertex is on the axis of symmetry we can proceed as follows:
Let's do an example.
Example 5
Graph f (x) = x2 – 2x – 3 by finding the x-intercepts and the axis of symmetry by factoring.
Solution:
y = x2 – 2x – 3 
y = (x – 3)(x + 1) 
x = 3 or x = – 1 when y = 0.
Since the x intercepts are – 1 and 3, the line through the mid point between them is the line with equation x = 1 and when x = 1, y = – 4.
So we know that the parabola opens upwards (a > 0), has vertex at (1, – 4), axis of symmetry is the line x = 1, and the x-intercepts are (3, 0) and ( – 1, 0). The graph looks like this:
Realize that x = ay2 + by + c is also a parabola. The only difference is that such a parabola would open sideways and its axis of symmetry would be parallel to the x-axis.
.
|quadratic function | general to standard form | x and y intercepts |
graphing from standard form | another approach to graphing | practice | solutions
.
1) For each of these parabolas
| a) f (x) = – x2 + 2x + 3 | b) f (x) = 3x2 + x – 4 | c) f (x) = – 2x2 + x – 1 |
(i) put the function rule in standard form f (x) = a(x – h) 2 + k
(ii) what are the coordinates of the vertex?
(iii) does f (x) have a maximum or minimum value?
(iv) what is f (h), the y-value of the minimum or maximum?
2) Find the x and y intercepts for:
| a) f (x) = – x2 + 2x + 3 | b) f (x) = x2 – 3x – 4 | c) f (x) = x2 – 8x + 5 |
3) Graph these parabolas:
| a) f (x) = – x2 + 2x + 3 | b) f (x) = x2 – 3x – 4 |
4) Use you knowledge for finding the maximum value for a parabola to solve this problem:
A farmer has 500 meters of fencing to enclose a rectangular field. If he wishes to enclose a maximum area, what dimensions should he make the field?
Hint: use the diagram to find an expression for the area of the field. This will be a quadratic expression which has a maximum. Put the expression in standard form and find h, the x coordinate of the maximum (diagram)
|quadratic function | general to standard form | x and y intercepts |
graphing from standard form | another approach to graphing | practice | solutions
..
1)
| a) f (x) = – x2 + 2x + 3 | b) f (x) = 3x2 + x – 4 | c) f (x) = – 2x2 + x – 1 |
| a = – 1, b = 2, c = 3 | a = 3, b = 1, c = – 4 | a = – 2, b = 1, c = – 1 |
| h = 1, k = 4 | h =
 , k =
 |
h =
 , k =
 |
| f (x) = – (x – 1) 2 + 4 |
 |
 |
| vertex at (1, 4) a = – 1 < 0 | vertex at
 |
vertex at
 |
| vertex is a maximum | vertex is a minimum | vertex is a maximum |
| max y-value = 4 | min y-value =
 |
max y-value =
 |
2) State the zeros or x-intercepts and y-intercepts for:
| a) f (x) = – x2 + 2x + 3 | b) f (x) = x2 – 3x – 4 | c) f (x) = x2 – 8x + 5 |
| y-int = c = 3 | y-int = c = – 4 | y-int = c = 5 |
| 3 + 2x – x2 = (3 – x)(1 + x) | x2 – 3x – 4 = (x – 4)(x + 1) | use the quadratic formula |
| x = 3 or x = –1 zeros | x = 4 or x = – 1 zeros |
 |
.
.
3) Graph these parabolas:
| a) f (x) = – x2 + 2x + 3 | b) f (x) = x2 – 3x – 4 |
Note: these are a) and b) from question 2 so we have the intercepts.
h is the mid-value of the zeros and k = f (h)
.
Since A(x) = x (250 – x), and this is the zeros form of this quadratic function,
we know the zeros are at x 1 = 0 and x 2 = 250, since these values make A(x) = 0
Therefore the axis of symmetry is half way between the zeros which is at x = 125
Since the maximum value for A(x) occurs on the axis of symmetry
x = 125 is the equation of the axis of symmetry.
Solution: make the field a square which is 125 meters per side to maximize the area.
.
|quadratic function | general to standard form | x and y intercepts |
graphing from standard form | another approach to graphing | practice | solutions
.
.
(all content of the MathRoom Lessons © Tammy the Tutor; 2004 - ).
