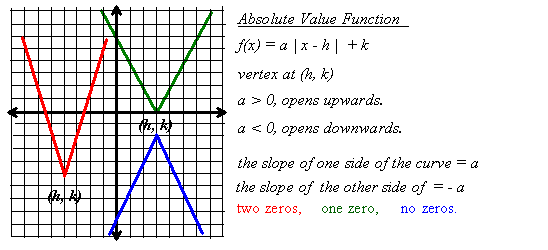
ABSOLUTE VALUE FUNCTION:

(very much like parabolas with straight instead of curved sides)

Absolute Value Function Properties Table
function: Absolute Value	rule: f(x) = a | x – h | + k	graph: V shaped
domain: unless reality dictates other	range: , a < 0 , a > 0	vertex: (h, k)
zeros: 0, 1, or 2 depends on variation	y-int: always unless reality dictates other	asymptotes:
increasing: x < h, if a < 0 x > h, if a > 0	decreasing: x > h, if a < 0 x < h, if a > 0	constant:
< 0: beyond 0's if a < 0, and k > 0 between zeros if a > 0, and k < 0	> 0: beyond 0's if a > 0, and k < 0 between zeros if a < 0, and k > 0	misc:

.

* absolute value function * function properties table * solving equations * inequalities * practice * solutions

.

Finding the Rule

To find the function rule for an absolute value function, we need 3 points on the graph.
If however one of those points is the vertex, we only need 2 points: the vertex and one other point.

Here are 2 examples illustrating the procedure for finding the function rule.

Example

Find the function rule for the absolute value function with vertex at (2, 1) through (5, 13).

Solution

Since the vertex is at (2, 1), we know that h = 2 and k = 1
Therefore f (x) = a | x – 2 | + 1 is the equation of the function.
Since (5, 13) is on the graph, we can replace x with 5 and f (x) with 13 to solve for a.
So, 13 = a | 5 – 2 | + 1 so 3a = 12 therefore a = 4.
The function rule is f (x) = 4| x – 2 | + 1.
The slope of the line on the left is – 4 and the slope of the line on the right is 4.

Example

Find the function rule for the absolute value function through (2, 5), (0, 5) and ( – 1, 7).

Solution

Note that (2, 5) and (0, 5) have the same y value. Therefore, due to the symmetry of the graph, we know that the x-coordinate of the vertex is midway between the x-values 2 and 0. Thus, h = 1, so now we only have to find k and a to complete the question.

We set up 2 equations in 2 unknowns (a and k) and solve.
Using the points (0, 5) and (-1, 7) we get:

5 = a | 0 – 1 | + k which becomes 5 = a + k
7 = a | – 1 – 1 | + k which becomes 7 = 2a + k

subtracting, we get 2 = a and substituting a = 2 into 5 = a + k we get k = 3
So the function rule is f (x) = 2 | x – 1 | + 3

For the next example, recall that x + h = x – (– h)

Example

Find the function rule for the absolute value function which passes through the points
(1, 17), (2, 21), and (–3, 9).

Solution

First, we will find the equation of the line joining (1, 17) and (2, 21), the right branch.

slope = so the equation of the line is

.

From this we know the slope of the left branch = – 4, the equation of the left branch is

y – 9 = – 4(x + 3) or y = – 4x – 3.

The vertex is the point of intersection of the two lines:

We solve y = 4x + 13 and y = – 4x – 3 for their point of intersection (the vertex).

When we add the 2 equations together, we get 2y = 10 so y = 5
Substituting y = 5 into y = 4x + 13 we get 5 = 4x + 13 so x = – 2
Since the x-value of the vertex = h, and the y-value of the vertex = k,
the function rule is f (x) = 4 | x + 2 | + 5.

SOLVING ABSOLUTE VALUE EQUATIONS:

Solve both equations to find the solution set.

** watch for | x – a | = – b since an absolute value cannot be negative, there's no solution!

.

FINDING ZEROS :

To find the 1, 2 or no zeros, we solve f (x) = 0 just as we would any absolute value equation.

.

Let's first discuss what absolute value means. Usually we learn that the absolute value of any number is the positive value of the number but that's not quite true. The words say it all. The absolute value of a number is the value of the number without regard to sign. The signs we attribute to numbers indicate a quality rather than quantity. When I say that the temperature is minus 3 degrees, I'm indicating that the temperature is 3 degrees below zero.

The minus sign indicates direction but has nothing to do with the value of the number.

So, when we talk about the absolute value of a number we are talking about how many items there are rather than what direction or quality that number has. Therefore, to find the absolute value of a number or expression, simply disregard the sign before the number or expression.

For instance, the absolute value of – 4 is 4. The absolute value of – (3x + 1) is 3x + 1.

If I'm told that the absolute value of an expression is equal to 5, then I know that the expression equals either + 5 or – 5 since both of these numbers have an absolute value of 5.

Absolute value is denoted by vertical lines on either side of the expression as in
the statement | x – 3 | = 9 , which is read " the absolute value of x minus 3 equals 9 ".
Let's solve this question as an example.

Since we know that the absolute value of x – 3 = 9,

we know that x – 3 must = either + 9 or – 9, so that's our first step,

then we solve the 2 linear equations for 2 solutions like this:

| x – 3 | = 9 becomes x – 3 = 9 or x – 3 = – 9

if x – 3 = 9 then x = 12

if x – 3 = – 9, then x = – 6.

Substituting x = 12 and x = – 6 satisfies the equation.

When there are two absolute value expression in the equation, we proceed the same way.

Here's an example:

Solve | 5x – 3 | = | x + 4 |

We rewrite as two equations: 5x – 3 = x + 4, .......and ........ 5x – 3 = – ( x + 4)

Now we solve the two equations: 5x – 3 = x + 4 becomes 4x = 7, so x = 7/4,

5x – 3 = – ( x + 4) becomes 6x = – 1, so x = – 1/6 .

Note: The absolute value of an expression cannot be negative, so | x + 7 | = – 4 is not an equation at all since the absolute value of anything cannot equal negative 4! Be alert. Watch for these things and don't waste time trying to figure them out. Just write no solution and move on!

* absolute value function * function properties table * solving equations * inequalities * practice * solutions

SOLVING ABSOLUTE VALUE INEQUALITIES

basic rule:

reverse the direction of the inequality

when we multiply or divide by a negative.

.

| f (x) | < a becomes – a < f (x) < a (thumbs in -- an interval solution)

| f (x)| > a becomes f (x) < – a and f (x) > a (thumbs out -- 2 separate solutions)

.

.

examples:

| 5 – 2x | < 7	| 3x + 6 | > 27
– 7 < 5 – 2x < 7	3x + 6 < – 27 or 3x + 6 > 27
– 12 < – 2x < 2	3x < – 33 or 3x > 21
*6 > x > – 1	x < – 11 or x > 7
– 1 < x < 6 soln: ] – 1, 6 [	solns:
less than so soln is an interval or thumbs in	greater than so soln is a union of disjoint intervals or thumbs out

* this statement is bad form -- correct form -- small (–1) on left -- big (6) on right.

.

* absolute value function * function properties table * solving equations * inequalities * practice * solutions

Practice

(make a diagram -- it helps!)

.

1)Find the function rule in Standard Form for the absolute value function:

a) vertex at (–3, 7), through (– 4, 8)

b) through the points (0, 9), (3, 14) and (5, 24)

c) through the points (1, 8), (7, 8) and (5, 4).

.

2) Solve | 2x – 11 | = 13

.

3) A submarine photographs a sunken shipwreck and then re-surfaces. The depth in metres of the submarine follows the rule D(t) = 15 | t – 8 | – 120, where t is the time in minutes that the submarine is submerged.

a) Make a graph of the situation respecting the realities of submarines.
(make the x-axis the surface of the water)

b) For how long is the sub under water in total?

c) How long does it take to get to maximum depth?

d) What is the maximum depth of the sub (in metres)?

e) How long is the sub deeper than 90 metres?

.

4)Thirteen months ago, Luke bought some stock whose price has varied according to the function rule P (x) = 1.25 | x – 5 | + 45 where x is the number of months since he bought the stock and P (x) is the price of the stock in dollars.(pay attention to the limited domain here)

a) When was the stock price at its lowest?

b) When was the stock price at its peak?

c) For how many months did the stock increase in value?

d) Over what months was the stock worth less than $50?

* absolute value function * function properties table * solving equations * inequalities * practice * solutions

Solutions

(make a diagram -- it helps!)

1)

a) vertex at (–3, 7), through (– 4, 8)
this function opens upward so "a" is positive.

Since we know the vertex, h = – 3 and k = 7 we need to solve for a.

a is the absolute value of the slope of the line through the vertex and (– 4, 8).

a = | (8 – 7) / ( – 4 + 3) | = 1.

Therefore the function is f (x) = | x + 3 | + 7

.

b) through the points (0, 9), (3, 14) and (5, 24)

The equation of the line through (3, 14) and (5, 24) is:

Therefore, the slope of the left side of the graph = – 5

The equation of a line through (0, 9) with slope – 5 is:

y = – 5x + 9 since (0, 9) is the y-intercept.

Now let's solve for the vertex; the intersection of y = 5x – 1 and y = – 5x + 9.

When we add the 2 equations, we get 2y = 8 so y = 4

Substituting into y = 5x – 1, we get 4 = 5x – 1 therefore x = 1

The function rule is f (x) = 5 | x – 1 | + 4.

.

c) through the points (1, 8), (7, 8) and (5, 4).

Since (1, 8) and (7, 8) have the same y-value, the x-value of the vertex is midway between them at x = 4.

Since (7, 8) and (5, 4) are both right of x = 4, the slope of the line through them = a.

Slope between (7, 8) and (5, 4) is 4/2 = 2.

Substituting (5, 4) into f(x) = a | x – h | + k, where a = 2 and h = 4 we find k.

4 = 2 | 5 – 4 | + k yields k = 2.

The function rule is f (x) = 2 | x – 4 | + 2.

.

2) | 2x – 11 | = 13 gives us

2x – 11 = – 13 2x = – 2 so x = – 1

or

2x – 11 = 13 2x = 24, so x = 12

.

3) a) D(t) = 15 | t – 8 | – 120

b) the sub is under water for 16 minutes (set D(t) = 0)

c) It takes 8 minutes to get to maximum depth. (t = 8 at the vertex)

d) Maximum depth = 120 metres since D(8) = – 120

e) Solve D(t) < – 90: We get 15 | t – 8 | – 120 < – 90

which becomes – 30 < 15( t – 8) < 30 ........ so 6 < t < 10.
The sub is deeper than 90 m for 4 minutes.

4) P(x) = 1.25 | x – 5 | + 45

a) When was the stock price at its lowest? 5 months after purchase ( x = 5 at min)

b) When was the stock price at its peak? 13 months after purchase (incr on x > 5)

c) For how many months did the stock increase in value? 8 months (from 5th to 13th)

d) Over what months was the stock worth less than $50?

Set P(x) < 50 to get 1.25 | x – 5 | + 45 < 50

| x – 5 | < 4 , so – 4 < x – 5 < 4

1 < x < 9

The stock was worth less than $50 from the 1st to the 9th month.

.

* absolute value function * function properties table * solving equations * inequalities * practice * solutions

( Functions MathRoom Index )

(all content © MathRoom Learning Service; 2004 - ).