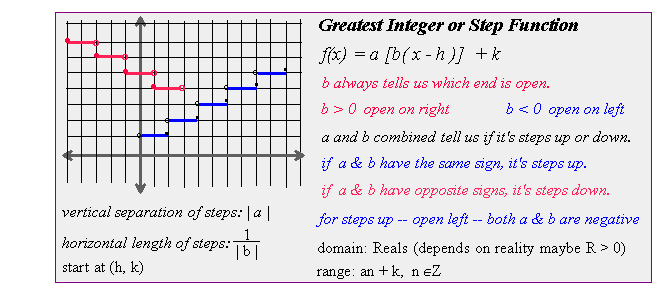
| the Greatest Integer (Step) Function |
Greatest Integer or Step Function:
A function in use daily by all kinds of businesses is the "step" function, so called because it looks like steps. Postal rates, car rental rates, long distance and courrier rates as well as sales commissions are all based on a step function.
As we can see, the "curve" is made up of a series of separate steps that either increase (steps up) or decrease (steps down) throughout the domain.
The range values (y's) are integers -- positive or negative whole numbers -- no fractions.
Note: [ n ] indicates the greatest integer part of n
If n = 6.357, then [ n ] = 6
We must be careful left of zero in the negative integers: [ - 9.2] = - 10
The easiest way to do it is note the last whole number we passed when
we moved on the number line from left to right. ______-10____-9.2_____________-1___

Unlike the square root function, where a tells us up or down and b tells us left or right, the properties determined by the parameters a and b in the step function are found by considering both their signs. (see info in diagram re. a and b).
Let's analyze a step function.
.
Example 1
f(x) = 5 [2x - 6] + 1
We put it in standard form by factoring the 2 t f(x) = 5 [2(x - 3)] + 1
Now, a = 5, b = 2 and (h, k) is (3, 1).
Since a and b are both > 0, it is steps up, open on the right
The vertical separation is 5 units, and the horizontal length of a step is ½ unit.
We start at (3, 1), run horizonatally for ½ a unit, then jump 5 units vertically
to (3.5, 6) and then we make another step ½ a unit long, etc. (try graphing it)
Now a word problem.
Example 2
A salesman earns $750 salary per week and a $50 bonus for every $600 sold during the week.
How much will he earn in a week if his sales total is $1790?
The step function here is determined this way.
What does his boss do to figure out his salary? He divides the sales total by $600,
to find out how many $50 bonuses to include, then he adds $750.
The function rule is:

In a week when his sales total $1790, we replace x to get

Had our salesman sold just $10 more, he would have made 3 bonuses instead of 2.
Since 1790 / 600 = 2.ta-da..., he will make 2 bonuses.
We only consider the integer part -- not the ta-da...
That's why it's called the greatest INTEGER function.
Example 3
At the end of December, Chucky's mom lends him $350 dollars to attend
a hockey tournament. He agrees to repay the loan at $50 per month
on the 1st of each month starting January until the debt is repaid.
If t represents the number of months he's been repaying the loan:
a) Write the function rule that represents the amount still owed.
b) what is the domain of this function?
c) How much does Chucky still owe his mother on April 15th?
d) Graph the function over its entire domain.
Solution
a) The debt starts at $350 and decreases by $50 every 1st of the month.
So, f(t) = - 50 [ t ] + 350 ; t ` Z
b) the domain is [0, 7] since it will take 7 months to repay the $350 at $50/month.
c) On April 15th, t = 4, so Chucky will have made 4 payments. He still owes $150.
d) a = - 50, b = 1, so it is steps down, open on the right.

.
Practice
1) a) Put these function rules in standard form
b) list the vertical separation (vs), and horizontal length (hl) of the steps.
| i) f(x) = [ 3x + 5 ] | ii) f(x) = 3[ 7 - 2x ] - 6 | iii)  |
2) An educational consultant is making up questions for the final math exam.
The exam requires 250 questions and he submits 25 questions per week.
a) What is the rule for the function for the number of questions remaining to submit.
b) How many questions are left to submit 50 days after his first submission?
c) Graph the function.
Solutions
1)
| i) f(x) = [ 3x + 5 ] f(x) = [ 3(x + 5/3) ] vs = 1 unit hl = 1/3 unit |
ii) f(x) = 3[ 7 - 2x ] - 6 f(x) = 3[- 2[x - 7/2 ] - 6 vs = 3 units hl = 1/2 unit |
iii)  f(x) = [1/5( x - 100) ] + 3 vs = 1 unit hl = 5 units |
2) This is really the same question as Chucky and his mother with the loan (example 3).
Here, we start at 250 questions to submit and reduce that number by 25 per week until they've all been submitted.
a) a = - 25; b = 1 ; h = 0 and k = 250
So, f(t) = - 25 [ t ] + 250 ; t ` Z; t in weeks
b) Since 50 days = 7.something weeks, he will have submitted 7(25) questions.
There are 250 - 7(25) = 75 questions.
c)

.
.
Back to Functions MathRoom Index
.
.