| The First Degree Rational Function (fractions) |
Rational Functions (Fractions)
Rational comes from ratio -- ratios are fractions-- division.
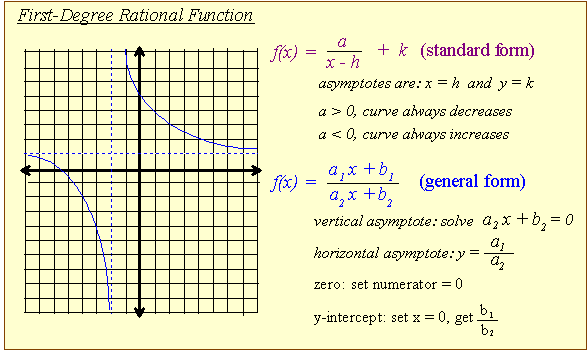
Asymptotes
The first degree rational function always has two asymptotes
one vertical and one horizontal.
The vertical asymptote occurs because there is a value of x that makes the denominator equal zero -- and division by zero is undefined in our number system.
The horizontal asymptote is best understood with limits in Calculus.
It defines the value y approaches as the x-values head for either end of the axis, that is: x gets extremely small or extremely large.

Note: asymptotes are LINES so we have to write an equation.
We cannot write "the vertical asymptote is 4". We must write x = 4
As we see, the domain and range would both be R if there were no asymptotes
so we describe them exactly that way. We eliminate the asymptote value like this:
domain:  |
range:  |
If reality dictates, the domain and range could be limited to only positive values.
.
From General to Standard Form
Though I much prefer to work with the general form of the rule, we should know how to change from one form to the other. The fraction tells us how -- we have to divide -- then make a minor modification once we're done.
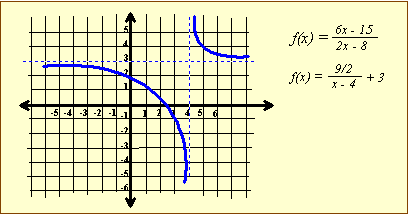
Example 1
Put this rational function rule of correspondence into standard form:

We will divide 6x – 15 by 2x – 8.
The quotient gives us k and the remainder gives us a -- after the modification.

Now our only problem is that we don't have x – h in the denominator, we have a multiple of it.
So, we factor out 2 from 2x – 8, then we divide the 9 in the numerator by 2.
Now, we have standard form:

Since a = 9/2 > 0, the curve is always DECREASING (rational functions are backwards)
The vertical asymptote is x = 4 and the horizontal asymptote is y = 3.
The domain is  range:
range: 
The y-intercept is 15/8 (set x = 0) and the zero is 5/2 (set the numerator = 0)
Let's graph it.
Now one from the general form (easiest in my opinion)
Example 2
Describe the properties and draw the graph of 
Vertical Asymptote: set 2x + 6 = 0 so x = – 3 is VA
Horizontal Asymptote: ratio of the coefficients of x, so y = ½ is HA
y-intercept: set x = 0, we get (0, – ½);
x-intercept: set numerator = 0 we get (3, 0)
once we have the intercepts, we know the curve is increasing.

Finding the Inverse Function
In this case, we'll first solve for x, then switch the x's and y's, like this:
Example 3 Find the inverse function


.
Practice
1) Find the zero and the y-intercept for 
2) List the vertical asymptote, horizontal asymptote, y-intercept and zero for:
(remember asymptotes are lines -– they have equations!!)
a)  |
b)  |
c)  |
d)  |
3) Find the inverse function for 
4) John calculates his average hourly profit doing landscape work with the rule
 ,
,
where P(x) is the average hourly profit and x is the number of hours he works.
5) a) Graph and describe the properties of  .
.
![]()
Solutions
1) x = – 5/2, y = 5
2)
a)  VA: x = 1 |
b)  VA: x = 7/2 |
c)  VA: x = 1/2 |
d)  VA: x = 1 |
3) Find the inverse function for 
Switch x and y's:  , then cross-multiply: x (y + 9) = 2y – 5.
, then cross-multiply: x (y + 9) = 2y – 5.
we're trying to find y, so we multiply out the bracket and put the y-terms together on one side:
xy + 9x = 2y – 5 so we transpose to get
xy – 2y = – 9x – 5.
Now we factor out y, and divide both sides by it's coefficient:
y(x – 2) = – 9x – 5, so the inverse function is 
4)
| a) P(x) = 0, so x = 3 make numerator = 0 |
b) P(8) = $12.50 | c) maximum < $25 since the horizontal asymptote is y = 25 |
5)a)

Domain: |
Range: |
f (x) > 0 x < – 7/3, or x > –1 |
f (x) < 0 –7/3 < x < –1 |
b) 
so we're really considering the signs of y = (x + 5)(x + 1).
the zeros are at x = – 5 and x = – 1 -- and since this parabola opens upward,
the y-values are negative (< 0) between the zeros.
The solution is – 5 < x < – 1 .
![]()
(all content © MathRoom Learning Service; 2004 - ).