SQUARE ROOT FUNCTION:

( a semi-parabola.)

b = ± 1 so you factor out any other value.

ex:

had the 4 in the square root been a – 4 we still extract the root of 4 but b would = – 1.

Square Root Function Properties Table
function: Square Root	rule:	graph: semi-parabola
domain: x > h if b = +1, x < h if b = – 1,	range: y < k , a < 0, y > k , a > 0,	vertex: (h, k)
zeros: 0, or 1, depends on variation	y-int: 0, or 1, depends on variation	asymptotes:
increasing: for all x if a > 0	decreasing: for all x if a < 0	constant:
< 0: when f (x) < 0	> 0: when f (x) > 0	misc:

SOLVING SQUARE ROOT EQUATIONS:

NB: Solutions must be checked and only the principal (positive) square root is allowed.

To solve an equation with square roots:

isolate a square root and square both sides.

If either side is a binomial SQUARE IT PROPERLY AS A BINOMIAL!!

Example

substitute x = 4: ü

substitute x = ¾ so x = ¾ is not a solution.

For lessons, examples, and practice on solving radical equations, see Lesson 6.4. in The Algebra MathRoom.

Solving Square Root Inequalities

We solve these inequalities -- like always -- respecting the basic rule:

reverse the direction of the inequality

when we multiply or divide by a negative.

There are 2 other issues to consider with square roots since

1) we have to square things in order to free the variables from the radical sign. Squaring is a dangerous operation since it can turn lies into truths -- like politicians.

– 7 = 7 is not true

but, when we square both sides ....

49 = 49 is true!!

this is why we must check our solutions when working with even roots.

2) The even root places restrictions on the domain of the function.

If the root in question is only defined for x > 3 and our solution is x < 7, we have to include the domain restrictions in our answer. So, the solution interval would be 3 < x < 7

example: Solve this square root (radical) inequality

the domain of is x > – 1

Squaring both sides gives: 9( x + 1) < (2x – 3) ²

This gives us that: 9x + 9 < 4x ² – 12x + 9 ((a binomial) ² = a trinomial!!!)

Once we transpose: 4x ² – 21x > 0

We factor: x ( 4x – 21) > 0

Now either make a number line and test values for the product to be positive ( > 0 ) or

Analyze x (4x – 21) graphically like this:

y = 4x ² – 21x defines an upward opening parabola (quadratic)

with zeros at x = 0 and x = 5.25

The positive y-values occur left of 0 and right of 5.25

Solution: since we want just > 0 and not = 0, we can't include the endpoints:

we also can't include x's not in the domain (x's < –1) so,

the solution is –1 < x < 0 union with x > 5.25

When we check, we find that only x > 5.25 is a valid solution.

.

Finding the Rule

See MathRoom Functions: Finding the Rule, example 3

Word Problem

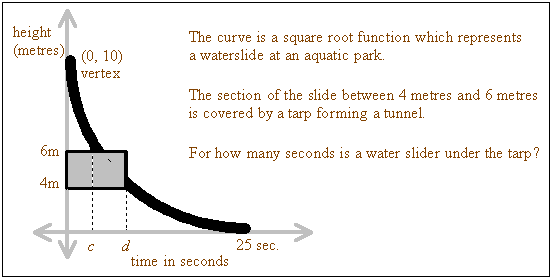
With any function problem, once we have the rule of correspondence, there's really only 2 things we can be asked. Either we know a y-value(s) and we need to find an x-value(s) or vice versa.

So, here, once we find the rule, we need to find the time lapse between the 2 x-values (c and d) paired with 6 metres and 4 metres in height.

Solution:

vertex is (0, 10) -- curve moves right so b = 1 -- point P is (25, 0).

So our first version of the rule is :

Plug in x = 25 and f (x) = 0: , so 5a = –10 and a = – 2

Which means that .

Now we set f (x) = 6, and f (x) = 4 in order to find c and d.

If, , so c = 4.

If, , so d = 9.

A water slider is under the tarp for 5 seconds.

.

Practice

1/ Put these square root function rules in standard form.(reminder: b = ± 1)

a)	b)
c)	d)

2/ List the values for parameters a, b, and vertex ( h, k ) for the 4 functions in question #1.

3/ List the function properties: (domain, range, intercepts, vertex, variation, signs)
for the 4 functions in question #1.

4/ Make a graph for the function rules in #1 parts (a) and (c).

5/ State the rule and any restrictions for the inverse of these square root functions:

a)	b)
c)	d)

6/

The diagram depicts the dining room of a hotel.
The red curve which defines the roof is a square root function with
rule of correspondence as shown.

a) Find the distance between the hotel and the dining room.

b) Find the height of the rectangular wall of the dining room facing the hotel.

c) How high above the ground is the BASE of the flagpole?

.

.

Solutions:

1/ Put these square root function rules in standard form.(reminder: b = ± 1)

a)	b)
c)
d)

2/

a) a = 6	b = 1	(h, k) = ( – 2, – 3 )	b) a = 2	b = – 1	(h, k) = ( 1, 2 )
c)	b = 1	(h, k) = ( – ¾ , 0 )	d) a = –¼	b = – 1	(h, k) = ( 32, 1 )

3/ a)

domain: a) x > – 2 or b) x < 1 or c) x > – 3/4 or d) x < 32 or	range: a) y > – 3 , or b) y > 2, or c) y < 0 or d) y < 1 or	vertex: a) (h, k) = ( –2, –3 ) b) (h, k) = ( 1, 2 ) c) (h, k) = ( –3/4, 0 ) d) (h, k) = ( 32, 1 )
zeros: a) ( – 7/4, 0) b) no zero; a > 0 and k = 2 c) ( – ¾, 0 ) d) (16 , 0)	y-int: a) b) ( 0, 4 ) c) d)	increasing: a) b) never. c) never. d) .
decreasing: a) never. b) . c) . d) never.	negative (< 0): a) [ –2, –7/4 [ b) never; g(x) > 0 ¼ x c) ; d)	positive ( > 0): a) b) c) never, h (x) < 0 for all x d) ] 16, 32 [

4/ a) Vertex (–2, –3) moves up and right.

c) Vertex (– ¾, 0) moves down and right.

5/ State the rule and any restrictions for the inverse of these square root functions:

a) now square and solve for y. so, Now, restrictions: x > 3; and y < 1.	b) we isolate the root so, square, solve: restrictions: x < 2; and y > 3.
c) we square and solve to get: restrictions: x < –7; and y > –4.	d) Now, restrictions: x < –5; and y < 2.

6)

In standard form, the rule of correspondence is:

a) The distance between the hotel and the dining room = h = 5 metres.

b) The height of the wall = k = 6 metres.

c) The height of the flagpole base is the y-value at x = 14 metres (5 metres + 9 metres).
setting x = 14, we get the flagpole base is 12 metres high.

( Functions Mathroom Index )

(all content © MathRoom Learning Service; 2004 - ).