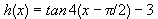Graphing Tangent Curves:
The curve for y = tan x is very different from the cosine and sine curves.
Since tan x equals the ratio of opposite over adjacent, we find values for tan x
from the unit circle since the y coordinate is sin x and the x coordinate is cos x.
Notice that when cos x = 0, at 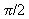 and at
and at 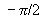 the tangent value is undefined since
the tangent value is undefined since
we're dividing by zero. Division by zero, though undefined in our number system,
is given the value 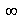 when the numerator is positive, and
when the numerator is positive, and 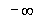
when the numerator is negative.
So, 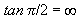 whereas
whereas 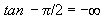 .
.
The tangent curve has asymptotes at those two values.
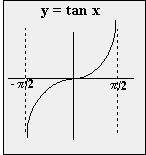
y = tan x is a cyclic curve like those of sin x and cos x,
however, as you can see there is no amplitude.
The period is 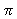 and the range is R.
and the range is R.
The only parts that move are the point of inflection at (0, 0) and the asymptotes
(A point of inflection is one where the curve changes its shape.)
Properties of Tangent Graphs
The transformed tangent rule is f (x) = a tan b (x – h) + k
period:  |
range: R |
asymptotes:  |
pt. of infl: (h, k) |
| a > 0, increasing |
a < 0, decreasing |
f (x) < k on half the period |
f (x) > k on half the period |
the asymptotes are at the ends of the period, (h, k) is the midpoint of the interval.
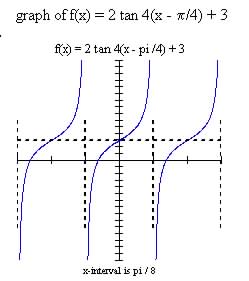
Let's graph 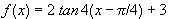 ,
,
period = 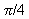 , the point of inflection will be at
, the point of inflection will be at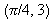
there will be an interval of 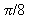 on either side of the point of inflection.
on either side of the point of inflection.
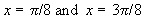 are the asymptotes.
are the asymptotes.
The curve will rise more steeply than the basic curve since a = 2.

Practice
1) For each of these tangent functions list :
.
2) Draw the graph of 1c) above.

Solutions
1)
a)  i) period =  ii)  iii)  |
b)  i)period =  ii)  iii)  |
c)  i)period =  ii)  iii)  |
2) 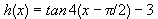
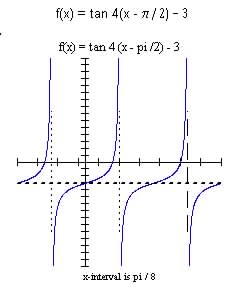
.
.
Trig MathRoom Index

(all content of the MathRoom Lessons © Tammy the Tutor; 2004 - ).
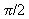 and at
and at 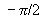 the tangent value is undefined since
the tangent value is undefined since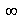 when the numerator is positive, and
when the numerator is positive, and 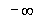
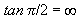 whereas
whereas 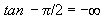 .
. 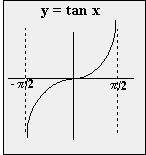
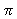 and the range is R.
and the range is R.

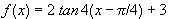 ,
,
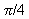 , the point of inflection will be at
, the point of inflection will be at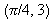
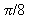 on either side of the point of inflection.
on either side of the point of inflection.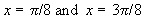 are the asymptotes.
are the asymptotes.