| SIMILARITY and CONGRUENCE |
Similar or Congruent: What's the Difference?
There are two kinds of human twins: dizygotic or fraternal twins (from 2 eggs) and monozygotic or identical twins (from 1 split egg). Fraternal twins look alike but it's easy to tell them apart -- because usually one is a boy and the other a girl. Identical twins are identical. They look exactly alike and are always the same gender. Sometimes, even their mother can't tell them apart.
In geometry, when we say figures are similar, we mean they look alike, but they are not identical – like fraternal twins, it's easy to see the difference between them. With similar figures, the shape is the same, however, the size is different. We could place one inside the other and line them up so that their corresponding sides are parallel.
Two congruent figures are exactly the same -- like identical twins. There's no way to tell them apart because they are identical. Congruent means "equal in all respects" so, everything – the sides, the angles, the perimeter, and the area are exactly the same. We could place one figure over the other and they would match up perfectly.

If 2 angles of one triangle are equal to
2 angles of another, the triangles are similar.
Since the 3 angles of a triangle add to 180°, the third angles must be equal by subtraction.
.
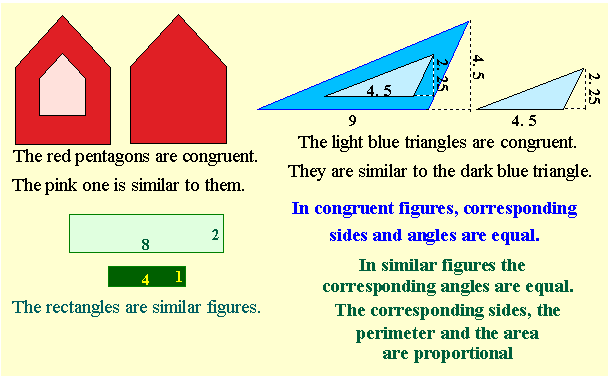
Similar Figures
The graphics software we use today to "draw" images with our computers, makes it extremely easy to create similar and/or congruent figures. To make the 3 blue triangles in the diagram above, I " drew" one of them, then I selected it, did a " copy and paste", to make the 2 congruent ones. Then, for the larger, dark blue triangle similar to them, I did another " copy and paste", changed the color to darker blue, and, with the grid showing on the drawing canvas, I stretched the small triangle, both horizontally and vertically, until the base and height were twice as big as before.
To create the green rectangles I "drew" the big one first, then I copied it and, using the grid, I shrunk or reduced the copy to half it's original size. In both cases, the ratio of the larger side to the smaller side is 2 to 1 and the ratio of the smaller side to the larger side is 1 to 2.

The perimeter of the large green rectangle is 20 units, the smaller rectangle's perimeter = 10 units.
The larger perimeter is twice the smaller. The smaller is half of the larger.
In similar figures, the ratio of the perimeters is equal to the ratio of the sides.
The area of the large green rectangle is 8 × 2 or 16 square units. The area of the small green rectangle is 4 × 1 or 4 square units.
The ratio of the areas is equal to the square of the ratio of the sides.
The ratio of the sides is called the proportionality factor.
We generally use c or k to represent it because
it can be called the proportionality CONSTANT.
For our rectangles, c = 2 for big side to little side and c = ½ for little side to big side.
Example:
1) Use the information in the diagram to answer the questions.

| a) Find angles C, Q, P and R? | C = R = 64°, Q = B = 30°, P = A = 86°. |
| b) Find the lengths of PQ and PR. |  , PQ = 2/3(5.7) = 3.8 in, PR = 2.2 in , PQ = 2/3(5.7) = 3.8 in, PR = 2.2 in |
| c) What is the ratio of BC to QR? | BC to QR = 3 to 2 |
| d) What is the ratio of PQ to AB? | PQ to AB = 2 to 3 |
| e) What is the perimeter of ABC? of PQR? | P for ABC = 15 inches, P for PQR = 10 inches |
| e) Find the "big to small" ratio of perimeters. | 15 to 10 = 3 to 2. |
| f) Find the area of each triangle. | Area ABC = ½(6 × 3) = 9 in², PQR = 4 in² |
| g) Find the "small to big" ratio of the areas? | small to big ratio = 4 to 9 or (2²) to (3²). |
.
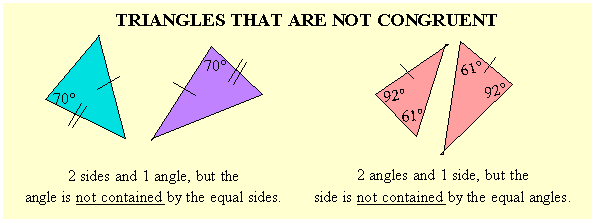
Congruent Triangles
There are 3 ways to show that 2 triangles are congruent,

Congruent triangles are also similar. The proportionality factor c = 1.
If 2 angles of a triangle are equal to 2 angles of another triangle,
the third angles are equal, so the triangles are similar.
If a side of one equals the corresponding side of the other,
the triangles are congruent.
![]()
Now get a pencil, an eraser and a note book, copy the questions,
do the practice exercise(s),then check your work with the solutions.
If you get stuck, review the examples in the lesson, then try again.
.
Practice Exercise
1) On grid (graph) paper, draw triangle TNE with angle T = 90°, TN = 8 squares, TE = 6.
Beside it, draw triangle CFA with angle C = 90° and CF = 4 squares, CA = 3.
a) Use a ruler to measure the lengths of the corresponding sides of the 2 triangles.
b) Use a protractor to measure the acute angles in both triangles.
c) What is the ratio of the sides of triangles TNE and CFA?
d) Find the area of triangle CFA.
e) How many times larger than the area of triangle CFA is the area of TNE? Explain.
2) a) Draw a small rectangle. Measure its dimensions. Calculate the Perimeter and Area.
b) Draw another rectangle with sides 3 times those of the first rectangle.
c) Calculate the Perimeter and Area of the bigger rectangle.
d) Describe how the perimeter and area of the rectangle changed when the side length
increased by a factor of 3.
3) Use the diagram to find the height of the tree.

.
Solutions
1)
a) Measuring in inches on ¼ inch grid paper, TN = 2 inches, TE = 1½ inches, EN = 2½ inches.
CF = 1 inch, CA = ¾ inch, AF = 1¼ inches.
b) angle E = 53° = angle A, angle N = 37° = angle F. These angles are complementary.
c) The ratio of the sides is 2 to 1.
d) Area = ½ b × h = ½ (1)(¾) = 3/8 inches².
e) The area of triangle CFA is 4 times larger than the area of TNE. The proportionality factor = 2 and the ratio of the areas = 2² = 4.
2) d) The perimeter of the bigger rectangle is 3 times that of the smaller.
The area is 9 times that of the smaller.
3) Use the diagram to find the height of the tree.

![]()