Polygons: Terms and Descriptions

Definition: a polygon is a dead parrot!

In a joke perhaps, but in geometry,

A polygon is a plane figure formed by 3 or
more intersecting line segments.

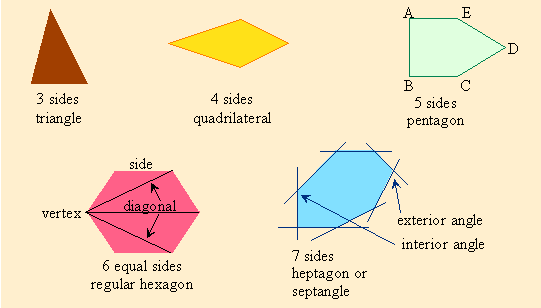
The lines are called sides and the point or corner where 2 sides meet is called a vertex (plural is vertices – pronounced vur – tih – sees). We label the vertices with upper case (capital) letters (see the green pentagon below). The line joining consecutive vertices is a side.

A diagonal is a line segment that joins any two non-consecutive vertices of a polygon (shown in the pink hexagon below).

A polygon of n sides has n interior and n exterior angles.
an exterior angle is formed by a side and the extension of an adjacent side.

In a Regular polygon all sides, all interior and all exterior angles are equal.

Regular triangles and quadrilaterals have special names.
A regular triangle is called an equilateral triangle.
A regular quadrilateral is called a square.

Naming Polygons

In almost every math book in which there is a discussion of polygons, we will see this statement:

polygons are named by the number of sides.

This is not quite true. The only polygon that is truly named by the number of sides is a quadrilateral, since quad as a prefix means four, and lateral means side. A lateral pass in football is a pass to the side instead of forward. Unilateral means one-sided and bilateral means two-sided.

All the other polygons such as a pentagon, a hexagon, and an octagon are named by the number of their vertices or corners. The suffix " gon" comes from the Greek word "gonia", which means corner or angle. However, since the number of corners in a polygon is always equal to the number of sides, we can continue to pretend that polygons are named by the number of sides.

But, really, we name polygons by the number of vertices or angles in them.
A triangle has 3 angles which it's name declares.
a pentagon has 5 angles and 5 sides, and a decagon has 10, etc.

The stop sign on the corner is a regular octagon -- with 8 equal angles and sides. The tiled walls and floors in our buildings and homes are made of regular polygons formed into patterns. Our yards, buildings, furniture and clothing designs are all shaped like various polygons so they are found all around us -- even in some of the sweetest places in nature.

Look at this pattern of regular hexagons!

Diagonals in a Polygon

As we said before, a diagonal of a polygon is a line segment that joins any two non-consecutive vertices of a polygon. We see them as lines crossing the inner space of the polygon. Now we'll figure out a formula to find the total number of diagonals in a polygon when we know how many sides -- oops! -- vertices there are.

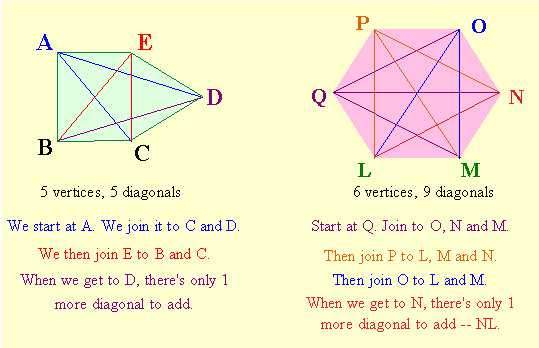
Let's investigate what happens as we join the diagonals around the vertices of the pentagon.

Since vertex A is joined to 2 other vertices -- B and E -- by sides, and vertex A can't be joined to itself to form a diagonal, we've identified 3 vertices that can't be the end of a diagonal from A. So since our pentagon has 5 vertices, we're left with 5 - 3 or 2 vertices to join with a diagonal line.
The same is true for vertex E. It can only be joined to B and C with diagonal lines. Then we get to D -- which is already joined to A, so we can only draw one diagonal, DB, from that vertex.

It's the same for the hexagon LMNOPQ. Both Q and P have 3 diagonals, O has 2 and N has only 1 diagonal left to draw.

The formula we use to find the total number of diagonals in a polygon of n sides is:

The (n - 3) part indicates that each vertex can be connected by a diagonal to 3 less than the total number of vertices. And the n/2 part says that each diagonal uses 2 vertices.
For our hexagon with 6 vertices, the number of diagonals is

For an octagon with 8 vertices, the number of diagonals is

.

Sum of the Interior and Exterior Angles of a Polygon

Let's look at an image so we can see the logic behind the theorem that says:

The sum of the interior angles of a polygon with n sides is
(n - 2) straight angles; or (n - 2)180°

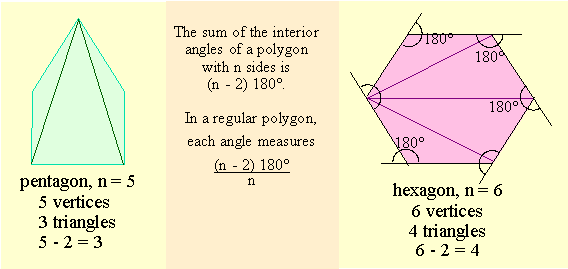
Since each vertex is connected to 2 other vertices by sides,
we will always get (n - 2) triangles from a polygon with n sides.
And since the 3 angles in a triangle sum to 180°,
the sum of the interior angles of a polygon of n sides is (n - 2) × 180°.
In a regular polygon, since the n interior angles are all equal,
each one measures (n - 2) × 180° ÷ n

With this formula, like all formulas, we can work backwards. Say we know that each interior angle of a regular polygon measures 144° and we want to know how many sides it has. We set
the formula equal to 144 and solve it for n like this:

then we solve like this: 180n - 360 = 144n, to get that 36n = 360 so n = 10

Now that we know the sum of the interior angles is always (n - 2)180°, we can find the sum of the exterior angles. From the hexagon in the diagram, we see that the sum of all the straight angles at the 6 vertices will be 6(180°). But the sum of the interiors is 4(180°). Therefore the sum of the exterior angles must be 2(180°) or 360°. This is true for all polygons, regular or not.
In a regular polygon, the exterior angles are all equal to ( 360°/n ).

The sum of the exterior angles of any polygon is 360° The degree measure of each exterior angle in a REGULAR POLYGON of n sides is

Note: Since the exterior and interior angles at any vertex are supplementary,
(they add to 180°,) the exterior angle is equal to 180° - (interior angle).

.

Example 1: For a regular dodecagon (12 sides), find:

a) The sum of the 12 interior angles.

b) The measure of each interior angle.

c) The measure of each exterior angle.

Solution: n = 12

a) The sum of the 12 interior angles = (n - 2)180° = 10(180°) = 1800°.

b) The measure of each interior angle = (1800°) / 12 = 150°.

c) The measure of each exterior angle = (360°) / 12 = 30° or (180° - 150°) = 30°.

Example 2:

Find the number of sides in a regular polygon if each interior angle measures:

a) 140° Solution: 180(n - 2) = 140 n 40n = 360 so n = 9 sides.

b) 157.5° Solution: 180(n - 2) = 157.5 n 22.5n = 360 so n = 16 sides.

c) 108° Solution: 180(n - 2) = 108 n 72n = 360 so n = 5 sides.

.

Formulas for a Polygon with n Vertices
Formula for	Formula
number of diagonals	.
number of triangles	n - 2
sum of interior angles	(n - 2)180°
sum of exterior angles	360°
each interior angle of regular polygon
each exterior angle of regular polygon

Now get a pencil, an eraser and a note book, copy the questions,
do the practice exercise(s),then check your work with the solutions.
If you get stuck, review the examples in the lesson, then try again.

Practice Exercises

1) Match each word in the list on the left with all the letters of all the figures it describes.
(there can be more than one match per word)

( solution )

2) Calculate the number of diagonals for each of the figures in #1.

( solution )

3) Explain how you would use ruler and protractor to construct a
regular hexagon with sides of 7 cm.

( solution )

4) Find the measure of each interior and exterior angle for:

a) A regular decagon.

b) A regular dodecagon (12 sides)

c) A regular septagon.

( solution )

5) Find the number of sides in a regular polygon if each interior angle measures 156°.

( solution )

.

Solutions

1)

2) Calculate the number of diagonals for each of the figures in #1.

a) n = 3 so 0 diagonals	b) n = 4, so ½n(n - 3) = 2 × 1 = 2	c) n = 3 so 0 diagonals
d) n = 7 so 14 diagonals	e) n = 5 so 5 diagonals	f) n = 5 so 5 diagonals
g) n = 6 so 9 diagonals	h) n = 8 so 20 diagonals

3) A hexagon has 6 sides. We draw a line segment and mark off AB = 7 cm.
Since each interior angle of a regular hexagon = 120°, we construct a 120° angle
at both A and B. Then we measure 7 cm to C on the right and F on the left. We contiinue
the process until we complete the hexagon.

.

4) Find the measure of each interior and exterior angle for:

a) A regular decagon. interior = 144° exterior = 36°

b) A regular dodecagon (12 sides) interior = 150° exterior = 30°

c) A regular septagon. interior = 128.57° exterior = 51.43°

5) We know that 156 n = (n - 2)180 which gives us 156 n = 180 n - 360
when we solve for n, we get 15 sides.

( Primary MathRoom Index )