Definition: a polygon is a dead parrot!

In a Monty Python's skit maybe, but in math,

a polygon is a closed figure with three or more straight sides.

A polygon of n sides has n interior and n exterior angles.

In a Regular polygon all sides are equal so all interior and exterior angles are equal.

We have names for polygons with a given number of sides such as triangle for 3 sides, quadrilateral for 4 sides, pentagon for 5, etc.

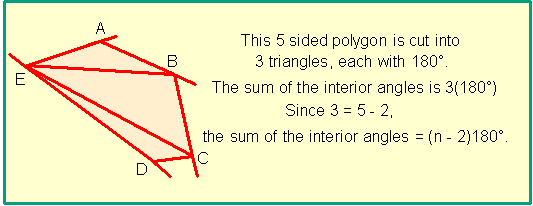
Sum of the Interior Angles of a Polygon

Let's look at an image so we can see the logic behind the theorem that says:

The sum of the interior angles of a polygon with n sides is
(n – 2) straight angles; or (n – 2)180°

Since we will always get (n – 2) triangles from a polygon with n sides, this theorem works for all polygons, and, in a regular polygon, the angles are equal,
so we can find the exact degree measure of each interior angle.

.

Now that we know the sum of the interior angles is always (n – 2)180°, we can find the sum of the exterior angles. From the pentagon in the diagram, we see that the sum of all the straight angles at the 5 vertices will be 5(180°). But the sum of the interiors is 3(180°). Therefore the sum of the exterior angles must be 2(180°) or 360°. This is true for all polygons, regular or not. In a regular polygon, the exterior angles are all equal to (360°/n).

Note: Since the exterior and interior angles at any vertex are supplementary, the exterior angle is equal to 180° – (interior angle).

.

Example 1: For a regular dodecagon (12 sides), find:

a) The sum of the 12 interior angles.

b) The measure of each interior angle.

c) The measure of each exterior angle.

Solution: n = 12

a) The sum of the 12 interior angles = 10(180°) = 1800°.

b) The measure of each interior angle = (1800°) / 12 = 150°.

c) The measure of each exterior angle = (360°) / 12 = 30° or 180° – 150° = 30°.

.

Example 2:

Find the number of sides in a regular polygon if each interior angle measures:

a) 140° Solution: 180(n – 2) = 140n 40n = 360 so n = 9 sides.

b) 157.5° Solution: 180(n – 2) = 157.5 n 22.5n = 360 so n = 16 sides.

c) 108° Solution: 180(n – 2) = 108 n 72n = 360 so n = 5 sides.

.

The Apothem and the Area of a Regular Polygon

The apothem of a regular polygon is the perpendicular
from the centre of the polygon to the midpoint of a side.

If we are given the lengths of the apothem and the "radius" like OB,
we use the Pythagorean Theorem to find s, the length of a side.

Similarly if given s, the length of a side and the "radius", we can find a the apothem.

Example 3:

Find the area of a regular hexagon with sides of 13 cm. and apothem of 5 cm.

Solution:

A hexagon has 6 sides so the area = ½ (6) (13) (5) = 195 cm².

Example 4:

The area of a regular polygon with side = 16 cm. and apothem = 8 cm. is 896 cm².
How many sides are there in the polygon?

Solution:

The area = ½ (n)(16)(8) = 896 cm² we solve and find n = 14 sides.

Example 5:

The side of a pentagon measures 8 cm. and the radius measures 5 cm.

a) Find the length of the apothem.

b) Find the area of the pentagon. (5 sides).

Solution:

a) Since the base of the right triangle formed by the side, the radius and the apothem equals half the length of the side, the base is 4 cm, the hypotenuse is 5 cm. so the apothem or height of the triangle measures 3 cm. (This is the famous 3, 4, 5 right triangle.)

b) The area = ½ (5)(3)(8) = 60 cm².

.

Practice

1) A regular hexagon has an area of 24 cm² and the apothem measures 3 cm.

a) How long is each side?

b) What is the perimeter of this hexagon?

(click for solution)

2) Find the area of a regular nonagon if the length of a side is 5.3 dm and the length of a line connecting the center to a vertex is 7 dm.

(click for solution)

3) Find the area of the following regular polygons:

a) pentagon: side = 8.2 m, apothem = 5 m.

b) hexagon: side = 9.4 dm, apothem = 3.2 dm.

(click for solution)

4) Explain how you would construct a regular hexagon with sides of 7 cm.

(click for solution)

5) Find the measure of each interior and exterior angle for:

a) A regular decagon.

b) A regular dodecagon (12 sides)

c) A regular septagon.

(click for solution)

.

.

Solutions

1) A regular hexagon with area = 24 cm², apothem = 3 cm.

a) side = 2.67 cm

b) perimeter = 16 cm.

.

2) area of nonagon if side = 5.3 dm and radius = 7 dm.

Use Pythagoras to solve for the apothem = 6.48 dm. so area = 154.55 dm².

.

3) Find the area of the following regular polygons:

1) pentagon: side = 8.2 m, apothem = 5 m. Area = 1025 m².

2) hexagon: side = 9.4 dm, apothem = 3.2 dm. Area = 90.24 dm².

.

4) A hexagon has 6 sides. We draw a line segment and mark off AB = 7 cm.
Since each interior angle of a regular hexagon = 120°, we construct a 120° angle
at both A and B. Then we measure 7 cm to C on the right and F on the left. We contiinue
the process until we complete the hexagon.

.

5) Find the measure of each interior and exterior angle for:

a) A regular decagon. interior = 144° exterior = 36°

b) A regular dodecagon (12 sides) interior = 150° exterior = 30°

c) A regular septagon. interior = 128.57° exterior = 51.43°

.

( Plane Geometry MathRoom Index )

(all content © MathRoom Learning Service; 2004 - ).