Pythagoras

Most math text books preceded this theorem with an introduction to the ancient Greek named Pythagoras who contributed this most famous triangle theorem. They all claim that he was a great mathematician -- the founder of the Pythagorean School of mathematics. But that's not the true story!! Pythagoras was never a mathematician. He was a frustrated musician. He composed songs, but, since he lived at a time before anyone had invented a language with which to write music, he was unable to jam with his buddies on his original compositions -- something musicians and especially composers, have loved to do throughout history. So, Pythagoras went to Egypt to study math because he realized that some new version of algebra -- which is a language -- could be transformed into code to write music.

After his studies in Egypt, Pythagoras returned to Greece where he established the Pythagorean School -- a school of music -- not mathematics. It was here that he invented the octave and the first version of the notation system we still use today to write music.

In this lesson, we discover his most famous mathematical theorem on right triangles which forms the basic theory of the branch of math called Trigonometry.

.

The Pythagorean Theorem

In a right triangle, the square on the hypotenuse
is equal to the sum of the squares on the other two sides.

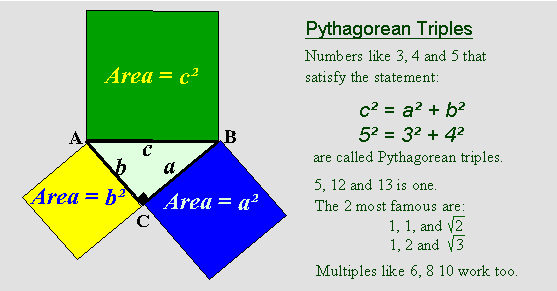
So, in the right-angled triangle ABC, c² = a² + b²

This statement can always be written in its two other forms:

c² – a² = b²

c² – b² = a²

So, given the lengths of two sides of a right triangle,
we can always find the length of the third side.

Note: Don't forget to take the square root of a², b² and c²

Note: the hypotenuse is always the longest side facing the 90° angle.
The sides around the right angle are called legs.
Either one can be considered the base or the height (altitude) when we need area.

.

Examples:

Find the missing side in these right triangles.

.

Practice

1) Find the missing side in these right triangles. Round to the nearest hundreth.

2) Which of these are Pythagorean triples? Justify your answer.

a) 3, 4, and 6

b) 15, 17 and 8

c) 13, 5 and 12

d) 8, 9 and 11

3) Make a diagram and solve each of these word problems.

a) A 7-meter ladder is leaning against the wall of a house so that
the foot of the ladder is 2 meters from the wall.
How far up the wall is the top of the ladder?

b) A ship leaves New York harbour and sails due East at 20 km/h for 2 hours.
It then turns directly south and sails at 25 km/h for 1 hour.
How far is the ship from New York harbour?

c)

The base of the great Pyramid of Khufu is a square with sides 230 m long.
What is the length of the diagonal of the base?

4) Find x to the nearest tenth of a centimeter.

.

Solutions

1) a)

b) This is the 3, 4, 5 triangle doubled so x = 10

c)

d) The Pythagorean triple 5, 12, 13 makes x = 12.

.

2)

a) 3, 4, and 6 -- NO 6² is not = 3² + 4²

b) 15, 17 and 8 -- YES 17² = 8² + 15²

c) 13, 5 and 12 -- YES 13² = 5² + 12²

d) 8, 9 and 11 -- NO 11² is not = 8² + 9²

.

3) a)

b)

.

3 c) Since when we draw the diagonal, we make an isosceles right triangle with
equal sides = 230 meters, the hypotenuse =

.

.

4) Find x to the nearest tenth of a centimeter.

Since the small triangle on the left is the famous 3, 4, 5 right triangle,
x² = 6² + 5² which means

.

( Plane Geometry MathRoom Index )

(all content © MathRoom Learning Service; 2004 - ).