
| Triangles: Angles and Sides |
Triangles and Angles:
The word triangle means 3 angles since "tri" is a prefix meaning 3 -- like in tricycle.
A triangle is a three sided closed figure formed when three non-parallel straight lines intersect one another. The point where two lines intersect is called a vertex (plural is vertices) which we label with uppercase letters.
The 3 vertices create three angles in a triangle whose sum is always 180° .

The longest side is opposite or facing the largest angle just as the
smallest side is opposite or facing the smallest angle.
Angle Definitions:
A right angle is exactly 90°. A straight angle is exactly 180°.
an acute angle: measures more than ( > ) 0° and less than ( < ) 90°.
an obtuse angle: measures more than ( > ) 90° but less than ( < ) 180°.
complementary angles: 2 acute angles that sum to 90° like 52° and 38°.
suplementary angles: 2 angles that sum to 180° like 152° and 28°.

.
Classification of Triangles:
Triangles can be classified either by using their angles, their sides, or both. For instance, a triangle with a 90° angle, in which two sides are equal to each other is called an isosceles right triangle. The word isosceles tells us that two sides are equal and the word right tells us that there is a right angle in the triangle. Now, we define the different classifications of triangles.
.
1/ By Their Angles
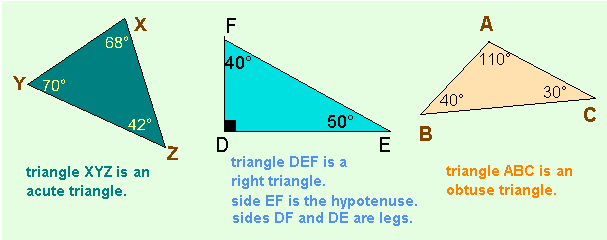
In an acute triangle, each of the 3 angles measures less than 90° but they always sum to 180°.
In a right triangle, there is one 90° angle and 2 complementary acute angles that sum to 90°.
The longest side is called the hypotenuse. The other two sides are usually called legs.
In an obtuse triangle, there is one obtuse angle and 2 acute angles.
.
2/ By Their Sides and Angles
In a scalene triangle, there are no equal sides and no equal angles.
In an isosceles triangle, there are 2 equal sides which create 2 equal angles.
In an equilateral triangle, there are 3 equal sides and 3 equal angles, of 60° each.

.
Now get a pencil, an eraser and a note book, copy the questions,
do the practice exercise(s),then check your work with the solutions.
If you get stuck, review the examples in the lesson, then try again.
Practice
1) Label these triangles acute, right, or obtuse. Find the missing angle measure x.
(reminder: the sum of the angles of a triangle is 180°)

2) Label these triangles scalene, isosceles, or equilateral. Find the missing side measure x.
(reminder: perimeter is the sum of the measures of the sides)

.
Solutions
1) Label these triangles acute, right, or obtuse. Find the missing angle measure x.

2) Label these triangles scalene, isosceles, or equilateral. Find the missing side measure x.

.
(all content © MathRoom Learning Service; 2004 - ).