Circular Solids: Cylinders, Cones and Spheres

These solids are based on circles. Cans, the columns on our buildings, storage tanks for liquids are all cylindrical shapes. Highway cones and dixie cups are conical shapes, and our planet and the balls we play with (except footballs) are spherical shapes.

Circle Formulas:(r = radius, d = diameter.)

Perimeter or circumference of a circle: ,

Area of a circle: ,

Cylinders:

A cylinder, is a pile of circles. A can is a cylinder. The base and top are circles, the sides or curved surface is a rectangle that has been wrapped around the circles. We measure the radius and circumference of the circular base and the height of the rectanglular "sides".

Another way to write the formula for Area of a Cylinder is:

Cones:

A cone's base is a circular flat surface. The "sides" (curved surface) come to a point called the vertex. The line joining the vertex to the circumference of the circular base is called slant height (like in a pyramid), and the vertical distance between the vertex and base is called the height. Because it comes to a point (vertex) like a pyramid, the volume of a cone is 1/3 the volume of the cylinder with the same height and radius. (÷ 3)

The surface area of a cone is the area of the circular base plus the area of the circle sector that makes up the sides. The area of circle's sector depends on the measure of the vertex angle.

We find the area of a sector created by a central angle of a circle with this proportion

.

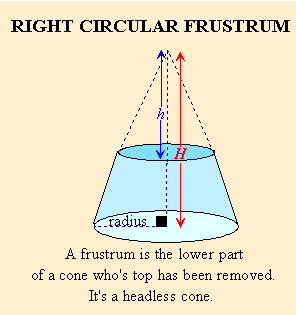
The volume of a frustrum is the volume of the entire cone minus the volume of the cone that's been cut off the top.

Spheres:

the height and radius of a sphere are equal so the only measure we need to find both Area and Volume is the radius.

A sphere or orb is the correct term for a ball or globe.
It has no flat surfaces. Half a sphere is called a hemisphere -- like the
Northern Hemisphere -- the upper half of the sphere on which we all live.

The curved surface of a sphere is made up of 4 circles. The lacing
on a softball almost outlines the 4 circular areas that make up the surface.

From this image, we can see how the sphere is made of 4 identical cones with bases on the
4 circular surfaces, with vertices meeting at the center of the sphere.

Decomposable Solids:

Find the area or volume of the separate parts then add them together.

Now get a pencil, an eraser and a note book, copy the questions,
do the practice exercise(s), then check your work with the solutions.
If you get stuck, review the examples in the lesson, then try again.

Practice Exercise

1)

2)

3)

4)

.

5)

6)

Solutions

1) bottom: hemisphere r = 10 cm. (½ of 20); top: cone r = 10 cm. h = 25cm.

Volume of hemisphere = ½ (Volume of sphere)

we get

Volume of the cone is

Total Volume = 2094.4 + 2618 = 4712.4 cm³.

2)

bottom: cylinder (open ended) r = 3 cm. (½ of 6), h = 12 cm.; top: hemisphere r = 3 cm.

a) total surface area is made of the sides of the cylinder and the top of the hemisphere

Total area =

b) volume = volume of cylinder + volume of hemisphere

Total Volume =

3) find volume.

bottom: prism w = 20 cm., l = 45 cm. h = 10 cm.; top: ½ cylinder r = 10 cm., h = 45 cm.

Volume of prism = 20 × 45 × 10 = 9000 cm³

Volume of ½ cylinder =

Total Volume = 16068.6 cm³.

.

4)

bottom: hemisphere r = 1.5 cm. (½ of 3); top: cone r = 0.9 cm. h = 2 cm.

Volume of hemisphere = ½ (Volume of sphere)

we get

Volume of the cone is

Total Volume =

5)

a) volume = volume of cylinder + volume of hemisphere

Total Volume =

b) Since we can't fill it to the top of the cap, the capacity is the volume of the bottom.
56.55 cm³ or centilitres.

6)

a) total Area = area of the sphere and sides of cylinder

sphere: r = 1.2 m; cylinder: r = 1.2 m., h = 5.4 – 2.4 = 3 m.

sphere:

cylinder sides:

Total area =

b) 1 litre covers 15 m² so we'll need 40.72 ÷ 15 = 2.71 litres -- 3 litres
we can't buy 0.71 of a litre.

c) Volume of the tank = volume of sphere + volume of the cylinder

Total Volume =

Since 1 m³ = 1000 litres, we multiply by 1000 to get 20 810 litres.

( Plane Geometry MathRoom Index )

(all solutions © MathRoom Learning Service; 2004 - ).