
| GEOMETRY PRIMER |
Introduction
The 3-dimensional space in which we live is made up of points, lines and angles. Points turn into lines, then lines become the sides or arms of angles when they intersect each other.
In everyday speech, most of us use the word "line" incorrectly. Geometry, however, demands that we use precise terms to define things, so let's learn to call lines, points and angles by their mathematically correct names.
One term we'll discuss that we generally use correctly is a ray.
Once we've heard the expression "a ray of sunshine" we know instinctively what it means.

Each ray of sunshine starts at the sun -- a point in space,
and continues on forever, in one direction.
Points and Lines
A point is a precise location or spot in space. We use a dot -- not a potato! -- to represent it, then we name or label it with an upper case (Capital) letter.
Here are 3 points labeled A, B and C.

When we join A to B, B to C and C to A, we have
3 line segments that define a triangle ABC.
In the diagram below:
CD or DC is a line -- a path of points extending forever in opposite directions.
We name or label a line by indicating any two points on it.
A line segment is a part of a line precisely defined and named by two endpoints.
ST is a line segment. X is the midpoint so SX = XT.
.
A ray is a part of a line that extends indefinitely in one direction from one endpoint.
We name or label it by the endpoint and any other point on it. QP is a ray.
Intersecting lines cross each other at a single point. Lines EF and GH intersect at J.
Perpendicular lines meet at right angles forming four 90° angles at their intersection.
OP is perpendicular to QR at point S. The small black square is used to indicate 90°.
Note: QP is a ray which has direction so we must name it in the correct order.
We can't call it ray PQ. In more advanced math courses, we'll call this ray a vector.
![]()
Angles

When you open your math book part way as in the picture, the bottom edge of the cover forms an acute angle with the bottom edge of the first page.
An angle is formed when 2 lines meet at a point.
The point at which the lines meet is called the vertex.
The lines that form the angle are called arms.
With our book, the bottom edges of the cover and first page are the arms and
the point where they meet on the book's spine, is the vertex .

In the diagram, point B is the vertex.
The line segments AB and BC are the arms.
BC is called the initial arm and AB is called the terminal arm.
It's as if BA started out lying on top of BC, pinned down at B.
Then we turned BA upwards to create the angle ABC.
Once we've got the cover of our math book open, we TURN the page. Turning is also called rotating -- so angles are the result of a rotation or turn. Think about the windshield wipers on the school bus. They rotate around a fixed point -- (if they didn't, they'd fly off the bus) -- through an angle large enough so that together, they wipe enough of the windshield for the driver to see clearly.
Naming Angles
We generally name angles like the one in the diagram above with 3 letters and we always put the vertex letter between the other two just the way it appears in the picture. The angle above can be named either ABC or CBA -- note that B, the vertex, is in the middle, between A and C. Sometimes, we use only 1 letter to name an angle, but that can be confusing when there's more than one angle at the same vertex.
In the diagram above, it's easy to see what angle we mean when we say angle B. But in the next picture, there are four different angles at B, namely angles ABD, ABE, DBC and CBE, so if I say angle B, which one do I mean? Therefore, it's best to use 3 letters to name an angle if there are many angles at a common vertex. In triangle XYZ, we know exactly which angle we mean when we say angle X, so in such a case, 1 letter will do.

.
Measuring Angles
When we open our first geometry kit, we see it includes a ruler, 2 right triangles, a set of compasses and a protractor (diagram). These tools allow us not only to measure but also to construct angles.
Ancient mathematicians and scientists used a sexagesimal system based on the number 60 to measure angles because they most often measured the circular motion of the sun, moon and stars. We still use it today on our clocks to tell time and to measure angles. On the clock, an hour (largest unit) is divided into 60 minutes, and each minute is divided into 60 seconds. When we measure angles, the largest units are called degrees instead of hours. The smaller units have the same names. The table of equivalences is:
1° (degree) = 60' (minutes) and 1' (minute) = 60" (seconds).
As always in math, there are symbols ( ° , ' , and " ) to represent degrees, minutes and seconds.
Since we're learning to measure angles in this lesson, we'll study how to use the protractor.

The 2 scales on a protractor, allow us to measure clockwise or counter-clockwise angles.The outer scale starts at zero (0) on the right near B and the inner scale starts on the left, near point A. The degree measures run in both directions to end at 180°. To measure an angle, we place point O on the protractor, directly over the vertex of our angle as shown. Here, angle BOD measures 45° and angle AOD measures 135° . We use the outer numbers to measure counter-clockwise rotations of point B and the inner numbers to measure clockwise rotations of point A. So angle AOC measures 25° (using the scale that begins at A) and angle BOC measures 155° (using the scale that begins at B).
Because angles BOD and AOD add to 180°, they're called supplementary angles.
Angle Definitions:
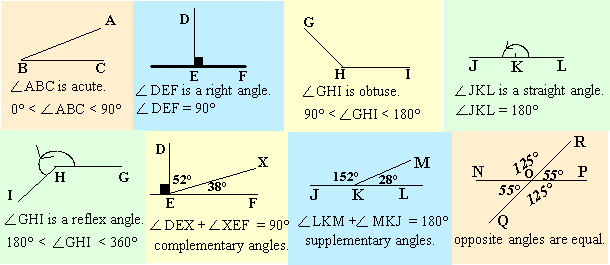
A right angle is exactly 90°. A straight angle is exactly 180°.
an acute angle: measures more than ( > ) 0° and less than ( < ) 90°.
an obtuse angle: measures more than ( > ) 90° but less than ( < ) 180°.
a reflex angle: measures more than ( > ) 180° but less than ( < ) 360°.
complementary angles: 2 acute angles that sum to 90° like 52° and 38°.
suplementary angles: 2 angles that sum to 180° like 152° and 28°.
opposite angles: also called "vertically opposite angles" are equal (look for a V).
.
Now get a pencil, an eraser and a note book, copy the questions,
do the practice exercise(s), then check your work with the solutions.
If you get stuck, review the examples in the lesson, then try again.
![]()
.
Practice Exercises
1) Match the words in the left column with the descriptions on the right.
| a ray | a) exactly 90° |
| acute angle | b) a part of a line precisely defined by 2 endpoints. |
| reflex angle | c) more than 90° but less than 180°. |
| straight angle | d) more than 0° but less than 90° |
| perpendicular | e) a point where 2 line segments meet to form an angle |
| right angle | f) more than 180° but less than 360°. |
| arm | g) part of a line from one endpoint extending forever in one direction. |
| line | h) meeting at right angles. |
| obtuse angle | i) a particular spot in space. |
| vertex | j) a line segment that forms one side of an angle. |
| point | k) exactly 180°. |
| line segment | l) a path of points extending forever in both directions. |
2)Label each angle acute, obtuse, straight, right or reflex.

3) Label each angle acute, obtuse, straight, right or reflex.
| a) 128º | b) 64º | c) 258º | d) 90º | e) 180º | f) 86º | g) 172º | h) 307º |
4) a) Find the complement for the acute angles in question 3.
b) Find the supplement for the obtuse angles in question 3.
5) Describe how to measure a reflex angle.
.
Solutions
1) Match the words in the left column with the descriptions on the right.
| a ray | g) part of a line from one endpoint extending forever in one direction. |
| acute angle | d) more than 0° but less than 90° |
| reflex angle | f) more than 180° but less than 360°. |
| straight angle | k) exactly 180°. |
| perpendicular | h) meeting at right angles. |
| right angle | a) exactly 90° |
| arm | j) a line segment that forms one side of an angle. |
| line | l) a path of points extending forever in both directions. |
| obtuse angle | c) more than 90° but less than 180°. |
| vertex | e) a point where 2 line segments meet to form an angle |
| point | i) a particular spot in space. |
| line segment | b) a part of a line precisely defined by 2 endpoints. |
2)
| angle A is acute | angle B is obtuse | angle C is reflex | angle D is right | angle E is straight |
3)
| a) 128º is obtuse | b) 64º is acute | c) 258º is reflex | d) 90º a right angle |
| e) 180º straight | f) 86º is acute | g) 172º is obtuse | h) 307º is reflex |
4 a)
| complement of 64º = 26° | complement of 86º = 4° |
4 b)
| supplement of 128º = 52° | supplement of 172º = 8° |
5) To measure a reflex angle, measure the obtuse angle or rotation,
then subtract that value from 360°
![]()
(plane geometry MathRoom index)
(all content © MathRoom Learning Service; 2004 - ).