| Similarity Practice |
1)
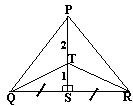
Use the facts given in the diagram to find the ratio of:
| a) ÊQTS to ÊTSR | b) ÊQTS to ÊQPS | c) ÊTRS to ÊPRS |
| d) ÊTQR to ÊPQS | e) ÊTSR to ÊPTR | f) ÊTSR to ÊPTQ |
.
2) In each of the diagrams, find values for x and/or y.
.
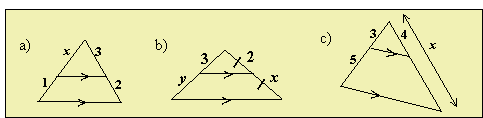
3) In the two diagrams shown here,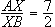 
. Find the value for x in both cases.
.
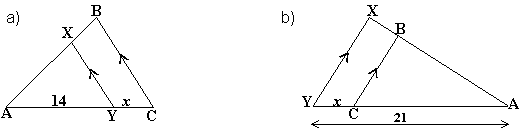
4) The sides AB and AC in ÊABC are divided at X and Y respectively in the ratio of 3:2. Find the ratio of ÊABC to ÊAXY.
.
5) The areas of two similar triangles are in the ratio of 16 to 25. What is the ratio of their corresponding sides?
6) AB and CD are the parallel sides of a trapezoid ABCD whose diagonals intersect at O.
Prove that ÊOAB Ã ÊOCD and list the equal ratios of corresponding sides.
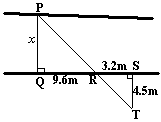
7) In order to find PQ, the distance across a river, we set up the triangle RST
with ST = 4.5 meters as seen here.
Use similar triangles to find the distance across the river.
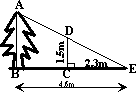
8) In order to find AB, the height of a tree, Harry, who is 1.5 meters tall
stands at C thus creating the similar triangles shown here.
Find the height of the tree.
.
.
.
.