 |
| ++ NEW SEASON MATH WELCOME ++ |
The academic year has begun -- and now that I'm not teaching in a school anymore, I miss meeting a group of new students for the first time. So I've decided to greet you, my readers, with the usual goings-on you would have witnessed had you been a new student in one of my math courses.
Once they were all seated and quiet, I would ask my students: "How many of you are completely convinced that math is impossible -- that you're not smart enough to understand the material in this course?" I rarely had to coax a response. Most of them thrust their hands up vigorously and grinned at me sheepishly -- as if to say -- "She really knows where we're at!"
"That's not fair!" was my unanticipated response. "If you people walk in here thinking that way, I haven't got half a chance of succeeding at my mission to teach you math, now have I? Give me a break!!" Invariably, they laughed. They'd never heard it put quite that way before. I then made them promise me that they'd psych themselves up to be smart whenever they were coming to math class. "You won't believe how easy math can be if you just adjust your attitude to "open" instead of "blocked". And one more thing. Open your ears. Listen to the math words because they tell you all you need to know."
"Next question. Who believes that math is absolutely useless in everyday life?" A few hands went up like a shot. These folks were thoroughly convinced that math had nothing to do with reality. I'd look at them seriously and ask "Do you shoot pool? Do you bowl? Do you buy stuff?" They'd answer "Yes." "Well, you need math to do all those things." Then I really got them interested. "Do you like music?" I'd ask. "Of course," they'd say "but what does music have to do with math?" "Music is the sound of math" I'd answer. And of course they'd ask "HOW?"
"What does the maestro do when he wants the orchestra to start playing?" I'd ask. After a second or so, someone would say "he counts." "Well if he counts, he's using math, isn't he?
Another thing. You've all heard about Pythagoras and his right triangle theorem; that he was a great mathematician. But most of you don't know that Pythagoras was never a mathematician. He was a frustrated musician. He composed songs but, since he didn't have a language with which to write his music, he was unable to jam with his buddies on his original compositions -- something musicians and especially composers, have loved to do throughout history. So, Pythagoras went to Egypt to study math. He realized that some new version of algebra -- which is a language -- could be transformed into a language to convey musical notes rather than words or mathematical concepts.
After his studies in Egypt, Pythagoras returned to Greece to establish the Pythagorean School -- a school of music -- not mathematics. It was here that he invented the octave and the first version of the notation system we still use today to write music.
Every note in a music score is a mathematical symbol that indicates what frequency to play and for how long to play it. Every rest represents a time interval too. Anyone who can't count or measure time, can't play music worth a damn!
When you look at a word sentence, it means something very specific to you; just as when a musician looks at a musical phrase." Check out some sheet music sometime. You'll see all kinds of numbers and symbols which closely resemble the kind of thing you see on a page of algebra text. There's shape, there's order, there's symmetry -- like diagrams in geometry, our number system, and the graphs we plot from those numbers.
This impressed most of them but there were still a few skeptics, so I told them this story:
I'm not only a math teacher. Amongst many other things, I'm also a singer/songwriter, record producer. The first time I solo-produced a recording project, we had a marvelous time putting down the 24 tracks of drums, vocals, guitar etc., but then, it was time to mix all that sound down to 2 track stereo. I had absolutely no idea what "mixing" meant, so we put the project on hold; I took home a cassette of the music we'd recorded and went to work trying to learn how to "mix". For 6 months, I listened to that tape from upstairs, from downstairs, with the head phones on, with the head phones off -- but I couldn't figure it out.
The "Eureka Moment" came on the second day of Christmas vacation. I was listening to the tape, trying to visualize an event similar to mixing sound. The image that came was of a huge paint mixing vat. I saw the recorded sounds I had to mix as different colored paints flowing into the vat. My job was to pick the mix or combination of colors that would produce the right effect. Just like mixing paint -- when you mix too much -- you get khaki brown -- no luster, no detail, just brown. If you mix too little, you get understated, shy color that doesn't say much. The trick was to find the balance, equilibrium, or the groove as musicians call it.
That's when it came to me. I had to graph the mix. I realized that I was trying to put symmetry to the sounds -- which were my variables. Symmetry for variables means a graph to me -- so I got a pad of graph paper, graphed my mix, called my recording engineer and told him to book some studio time. We were finally going to finish the project.
In the studio, I handed the graph to my engineer and said "Mix it like this." He did. I heard in my ears exactly what I had heard in my mind when plotting the graph. So math can make you a better record producer as well as a better bowler, shopper or pool shark. This comment was usually the clincher. They were convinced that math is an extremely useful thing every day of their lives.
So why do most people think math is just for geniuses -- that they could never get good at it? The reason students find math so hard to learn is that it demands discipline and vigilance at all times. Math has order and grammar rules like any language. The beauty of math language however, is that there are absolutely no exceptions to the rules. Unlike French or English, which include lists of exceptions, once you learn the parts of speech, order, and syntax of math language, you've got it covered. For example, in English, you could say: "Your boots -- put them on!", and though the order of the words is not quite right, you'd still be understood. In math however, this is not so. We can't write x - y when we mean y - x. They don't mean the same thing and no one can logically assume that they do except under certain circumstances which would have to be clearly predefined.
We also don't write intervals with the smaller value on the right and the larger value on the left. For instance, 5 < x < -3 is an unacceptable statement in math because the order is all wrong. A math phrase should evoke a logical, symmetric image -- this one evokes a Picasso image. The statement should be written like this: x < -3 or x > 5. Now we can see exactly where x lives on the number line, and more importantly, we can see that the sentence is talking about a union of two sets rather than a single interval between -3 and 5. Now we can see this image:
 |
Someone fluent in math language would see the same image if they read this sentence:
½ x å x c · ; | x - 1 | > 4
which says "There exists an x, such that x is a real number, and the absolute value of x minus 1 is greater than 4." Actually, the image above depicts the logical conclusion of the sentence rather than the sentence itself.
The sentence itself should evoke this image:
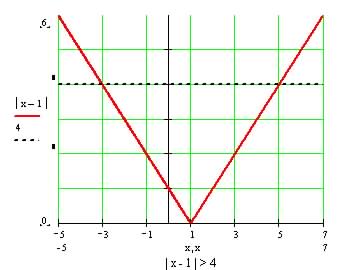
The dashed, black, horizontal line is at 4 on the y-axis, and since our statement says that the absolute value of x - 1 is greater than 4 we want to concentrate on the part of the red curve that is above this line. As you can see, the x-values found left of -3 and right of 5, generate the points on the red curve above the black line. Now we're looking at math TV -- there's audio in the algebra and video in the graph -- so, as with all languages, once you learn to speak math, you will be able to picture the images provoked by the "words".
To do well in math -- especially algebra -- you must become a nit-picker of the first degree. Every squiggle counts and one "oops" can screw up the whole works. With other languages, the same is not necessarily true. People can grasp your meaning from context when you speak to them enabling you to communicate your thoughts. In math however, you must say exactly what you mean. Not something like what you mean. The fastest way to learn a language is to speak it -- so speak your math whenever you can. As you write down the steps to a homework question, say it out loud! You'll become fluent in math and then you might even find it fun and exciting to do. Have a great semester.
TtT
.
.
.