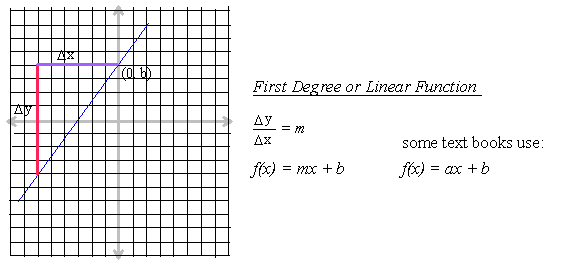
| Functions: Mathematical Models |
Mathematical Models or Function Templates
Mathematical functions are grouped into "families" or sets. Each "family" of functions has a unique shape (graph) and an equation (or function rule of correspondence) of specific form associated with it. For example, any quadratic function will, when graphed, show a parabola. The equation that describes this parabola will look like this (in standard form):
f(x) = a (x - h) 2 + k
and like this (in general form):
f(x) = ax 2 + bx + c
An absolute value function when graphed, will show a vee (V) and its equation in standard form, will look like this:
f(x) = a | x - h | + k
and so on.
The colored entries in the function rule are called parameters. It is their values that situate the unique set of points or locus (path) of the function in question.
Parameters
The parameter "slots" in a function rule are what we input to move the function around and determine its shape -- how quickly it rises or falls, where the vertex and the asymptotes are located.
A function rule is very much like this form:
| f(x) = | a | | x - | h | | + | k |
Once we choose what to put in the colored cells or to input for a, h and k -- we have fully determined the properties of the particular function.
Below,we see images of the "families" of functions we will discuss in the lessons of MathRoom Functions. Each is accompanied by a typical "function rule template" form for the function rule in standard form. The subsequent lessons in this MathRoom will explain the particular properties of the functions discussed.
.
1/ Linear Function (first degree)
.
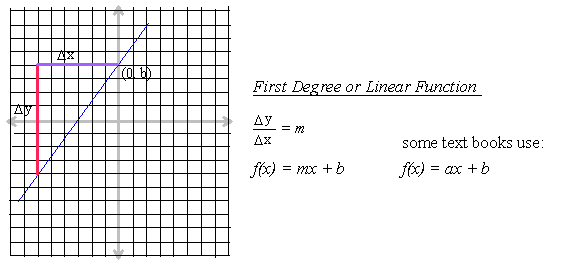
.
.
2/ Quadratic Function (second degree)
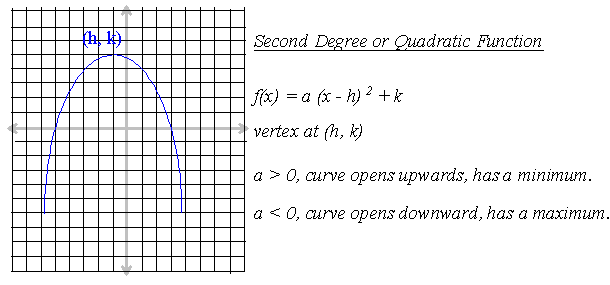
.
.
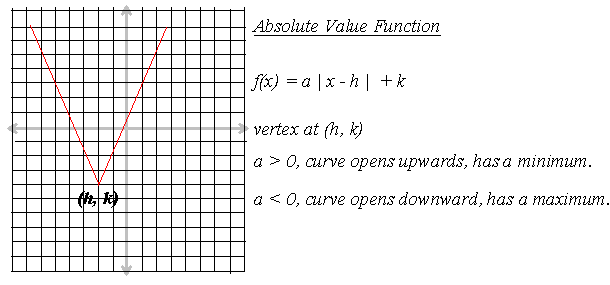
4/ Greatest Integer or Step Function
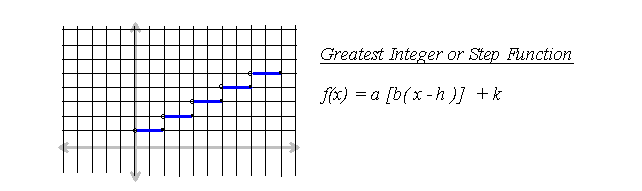

6/ First-Degree Rational Function
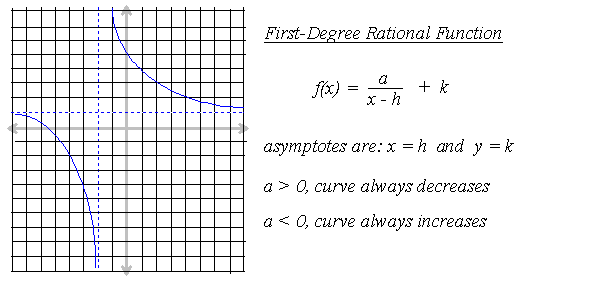
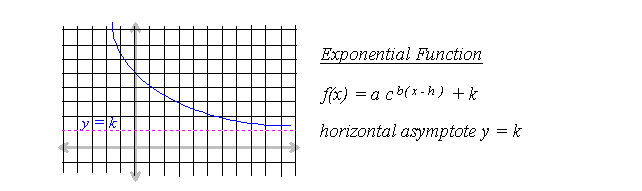
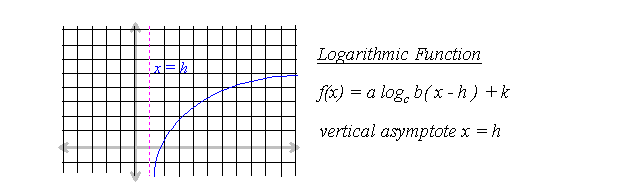


.
.
.
.
.
.
Notice the similarity between the 2 curves. If we haul the red y = sin x curve back (left) a quarter of a period (o/2 units), it will look exactly like the cosine curve. These two trig functions are related through the right triangle since the acute angles are complementary (add to 90º) -- so, the cosine of one will equal the sine of the other.
10/ Tangent Function
 Notice the asymptotes (vertical straight lines).
Notice the asymptotes (vertical straight lines).The lessons in MathRoom Functions will explain the details and properties of each of these families or sets of functions.
.
.