So, ( x – 3) (2x + 1) = 2x² – 5x – 3.
Do the 2nd step [(O × O) + (I × I)] as a single step for greatest efficiency.
Note: F × F refers to the First term in each bracket.
O × O and I × I refers to the Outer and Inner terms of the expression as a whole
L × L refers to the Last term in each bracket.
Using this technique, let's find the product of (3x + 2)(2x – 3)
F by F is (3x)(2x) = 6x²
(O × O) + (I × I) is (3x)(– 3) + (+2)(2x) = – 5x
L by L is (+2)(– 3) = – 6
So (3x + 2)(2x – 3) = 6x² – 5x – 6
| the product of two binomials in the same variables is a trinomial. |
The confusing part is that we change the name of the terms in each step.
for (3x + 1) (2x – 5)
in step 1, we call 3x and 2x the First terms.
in step 2, we call 3x an Outer term and 2x , an Inner term.
in step 2, we call +1 an Inner term and – 5, an Outer term.
step 3, we call +1 and – 5 Last terms.
In step 2 we look at the pair of brackets as a single unit.
step 1: (F __ )(F __ ), step 2: (O I)(I O), step 3: ( __ L)( __ L )
.
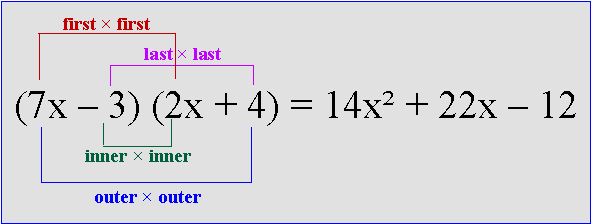
Here's another way to see it. Let's set the product up vertically instead of horizontally like we do when multiplying integers. The only difference is, we'll work from left to right instead of from right to left the way we do with integers.

Squaring a Binomial
Squaring a binomial such as (x – 5)² is the same as multiplying two binomials,
so the result is a trinomial.
Say we wish to find (x – 5)².
We know that (x – 5)² is (x – 5)(x – 5). With FOIL, we get x² – 10x + 25.
However, with a binomial, the product of the outer terms equals the product of the inner terms, since the terms in the brackets are identical.
Why not just double the product of the two terms in the bracket to get the middle term?
To square a binomial
step 1: Square the First Term,
step 2: Double the Product of the 2 terms ,
step 3: Square the Last Term.
So to find (x – 5)² : square x, multiply 2 times x times – 5, square (– 5)
The product is x ² – 10x + 25
note: Multiplication is commutative so in step 2, order doesn't matter.
note: Perfect squares are positive so if the first or last term is < 0 you goofed.
Examples
Perform the following operations
| a) (5x + 4)( 3x – 2) = 15x2 – 10x + 12x – 8 = 15x2 + 2x – 8 |
a) FOIL method: F by F = 15x2. O × O = – 10x, I × I = +12x, sum = 2x L by L = (+4)(– 2) = – 8 |
| b) (3a2 – 2b)(a2 – 7b) = 3a4 – 23a2b + 14b2 . |
b) FOIL method: F by F = 3a4 O x O = 3a2(– 7b) = – 21a2b I × I = (– 2b)(a2) = – 2a2b, sum = – 23a2b L × L = – 2b(– 7b) = + 14b2. |
| c) (4x – 6)2 = 16x2 – 48x + 36 |
c) square the 1st, 2 times 1st by last square the last |
.
Now get a pencil, an eraser and a note book, copy the questions,
do the practice exercise(s), then check your work with the solutions.
If you get stuck, review the examples in the lesson, then try again.
![]()
Practice
1/ Square these binomials in one step:
| a) (x – 7) 2 = | b) (3a – 2b) 2 = | c) (2x + y) 2 = |
| d) (2x 3 + 4) 2 = | e) (3y – 5z) 2 = | f) (6a + 5b) 2 = |
2/ Multiply using the FOIL method:
| a) (2x + 3)(4x – 5) = | b) (2 – 7x)(9 + 2x) = |
| c) (9m – 2n)(3m – n) = | d) (5x – 3y)(2x + 9y) = |
| e) (xy + 1)(3xy – 1) = | f) (2x + 3n)(2x – 3n) = |
| g) (4c – 5d)(c + 2d) = | h) (3m2 – 2n2)(2m2 – n2) = |
| i) (6t + 1)(3t – 2) = | j) (2m + 3t)(3m – 4t) = |
3/

The diagram shows an area rug on a hardwood floor with dimensions x and x + 3.
The rug leaves a border around the outside of the room.
The wider borders are 2 feet wide, the narrower ones on the sides are 1 foot wide.
- a) What is an algebraic expression for the area of the floor? (hint: A = l × w)
- b) What is an algebraic expression for the area of the rug?
- c) What algebraic expression represents the area of the border?
- d) If the value of x is 9 feet, find numerical values for parts a), b) and c).
.
![]()
Solutions
1/ Square these binomials in one step:
| a) x2 – 14x + 49 | b) 9a2 – 12ab + 4b2 |
| c) 4x2 + 4xy + y2 | d) 4x6 + 16x3 + 16 |
| e) 9y2 – 30yz + 25z2 | f) 36a2 + 60ab +25b2 |
2/ Multiply using the FOIL method:
| a) 8x2 +2x – 15 | b) 18 – 59x – 14x2 |
| c) 27m2 – 15mn + 2n2 . | d) 10x2 +39xy – 27y2. |
| e) 3x2y2 + 2xy – 1 | f) 4x2 – 9n2. |
| g) 4c2 + 3cd – 10d2 . | h) 6m4 – 7m2n2 + 2n4. |
| i) 18t2 – 9t – 2 | j) 6m2 + mt – 12t 2. |

3/ a) The area of the floor A = l x w is x (x + 3) = x 2 + 3x.
b) The dimensions of the rug are (x – 4 ) by (x + 1).
So, the area of the rug is (x – 4 ) (x + 1) = x 2 – 3x – 4.
c) The border's area is the difference between the floor's area and that of the rug.
So, the border's area is x 2 + 3x – (x 2 – 3x – 4 ) = 6x + 4
d) If the value of x is 9 feet, find numerical values for parts a), b) and c).
a) x 2 + 3x = 9 2 + 3(9) = 81 + 27 = 108 sq. ft.
b) x 2 – 3x – 4 = 9 2 – 3(9) – 4 = 81 – 27 – 4 = 50 sq. ft.
c) 6x + 4 = 6 (9) + 4 = 58 sq. ft.
.
(all content © MathRoom Learning Service; 2004 - ).
