not a function since when x = 9, f (x) = ± 3.
| PRE-CALCULUS FUNCTIONS REVIEW |
B/ Functions
To do Calculus well, we must be thoroughly familiar with the graphs and standard forms of all sorts of functions and their rules of correspondence. There's too many other things to do so we can't spend time making a table of values and plotting points. Therefore, all the functions covered in Maths 436 and 536 should be reviewed and practiced.
This lesson covers the basics. In depth lessons and practice on the functions we need are in the Functions MathRoom. Here, there's a workout on Domain, Range, and finding Inverse.
Before beginning a Calculus-1 course, we should be able to solve equations and inequalities efficiently for everything from a linear to a sinusoidal function.
.
| Definition |
| Graph Tests |
| Domain and Range |
| Inverse Functions |
| Exercise 2 |
| Solutions |
.
A function is a relationship between 2 variables:
x the independent variable (domain set) and
y the dependent variable (range set) such that
for each x-value there exists ONE AND ONLY ONE y-value.
so f (x) = 4x2 + 3 is a function since each x produces only one y but ![]() is
is
not a function since when x = 9, f (x) = ± 3.
If there is more than one value for f (x) from a single input x-value,
the relation is not a function.
.
Graph Test for a Function
A vertical line represents an x-value, so any vertical line on the grid that crosses the curve of a function does so only once. There will be exactly one y-value for the chosen x-value.
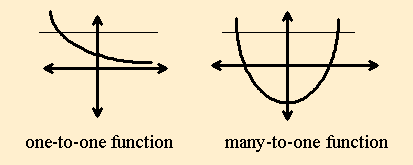
One to One and Many to One Functions
A one to one function returns any given range ( y) value once and only once.
A many to one function returns the same range ( y) value many times.
So f (x) = 5x + 3 is one-to-one but f (x) = x² is many-to-one.
A Linear function is always one-to-one unless it is a line parallel to the y-axis.
Graph Test for One-to-One or Many-to-One Functions
Once we know the curve is a function, we check the horizontal lines (y-values) of the grid. If any of them intersect the curve more than once, it is a many-to-one function.
.
The domain of a function is the set from which the function originates, the set of all possible independent variables, the x's. The range of a function is the set to which the function goes, the set of all possible dependent variables, the y's.
When we work with linear and quadratic functions, the domain is usually all Real numbers unless reality dictates otherwise. So, if the independent variable is t for time, domain elements can't be negative. Other functions such as rational, even root, exponential and logarithmic ones have limited domains and/or ranges because of their nature.
A rational (fraction) function has both vertical and horizontal (sometimes oblique) asymptotes; values of x and y that do not belong to the domain and range sets respectively. The vertical asymptotes are caused by values of the variable that make the denominator = 0. The horizontal asymptote is defined by the y-value the curve will approach as x becomes infinitely large or small; a number that y approaches but never hits. Oblique asymptotes are found with certain rational functions of degree greater than one.
For example, f(x) = (1 / x ) will never = 0 since a fraction's numerator must = 0 for the fraction to be 0. This numerator is always 1, so the horizontal asymptote of this curve will be the line y = 0 or the x-axis.
The exponential function always has a horizontal asymptote and the log function a vertical one because the base of these functions is always positive and we can't generate negative y-values from powers of a positive constant.
So, some of the things to look for when constraining domains are:
fraction denominators can't be = 0.
even roots can't be negative if we're working in R.
piecewise defined functions have segmented domains -- watch for undefined y's.
log and exponential functions have vertical and horizontal asymptotes respectively.
reality functions such as the parabolic flight of a projectile have Real Time/Space constraints.
Example: The domain of 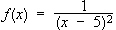 is
is 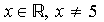 . The range is y > 0
. The range is y > 0
since f (x) is a perfect square, it's always greater than 0 (positive). This function is many to one since f (3) = f (7) = ¼. The y-value repetition is symmetric to the asymptote x = 5. We therefore constrain the domain elements to 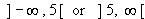 to make it one-to-one.
to make it one-to-one.
Example:
![]() is a function since we limit the y-values to positives or zero. Because it is a square root function, the expression under the root must be
is a function since we limit the y-values to positives or zero. Because it is a square root function, the expression under the root must be 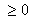 , so we need to define the x-values that make
, so we need to define the x-values that make 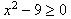 .
.
These are all real x-values between –3 and +3. This is a one-to-one function since we can only take the positive or principal square root.
The inverse of a function is the relation that maps the y-values of f (x) back to the x's that generated them. The domain becomes the range, and the range becomes the domain.
Unless defined on a restricted or constrained domain, the inverse of a many-to-one function is not a function because a given value of y will generate more than one value for x.
Say f (x) = x² , f (3) and f ( – 3) both = 9, so, f – 1(9) is either 3 or – 3 which means f – 1(x) is not a function. To find an inverse for f (x) = x2 we must first limit or constrain its domain.
If we set the domain condition 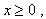 we eliminate the negatives from the domain.The function is now a semi-parabola, so it is one-to-one.
we eliminate the negatives from the domain.The function is now a semi-parabola, so it is one-to-one.
| TO FIND f – 1 (x): constrain the domain for f (x) if needed. 1) solve y = f (x) for x. or do it in the opposite order. |
Examples
| a) Linear Function y = 3x + 5 1-to-1 no restrictions y – 5 = 3x 1/3 ( y – 5) = x |
b) 3rd degree Polynomial y = x³ + 15 1-to-1 no restrictions y – 15 = x³ (y – 15)1 / 3 = x |
c) Square Root Function
constraints: x y² = x² – 9 gives y² + 9 = x², so |
| f – 1 (x) = (x – 5)/ 3 | f – 1 (x) = (x – 15)1 / 3 . |  |
(more on functions) (more on inverses)
Determine if the given expression is a function.
If yes, state its domain and range and if it is one-to-one or many-to-one.
1)  |
2)  |
3)  |
4)  |
5)  |
6)  |
7) Which of these curves are functions? State if they are 1-to-1 or many-to-1.
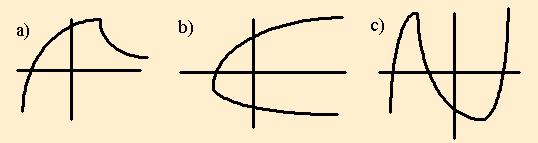
8) Find inverse functions for questions 2, 4 and 5 above.
State the constraints on the domain and range for the inverse function.
.
EXERCISE 2
1) not a function since (x – 7)1/2 can be > 0 or < 0.
2) yes a function. Domain:  |
Range: y m 0 | 1 - 1. |
3) yes a function. Domain:  |
Range: y  0 0 |
m - 1. |
4) yes a function. Domain:  |
Range: y  3 3 |
1 - 1. |
5) yes a function. Domain:  |
Range: y  0 0 |
1 - 1. |
6) yes a function. Domain:  , ,  |
Range: y  0 0 |
1 - 1. |
7) a and c are both many-to-one functions.
8)
| 2) Square Root Function constraints: y² = x + 3 is y² – 3 = x |
4) 1st degree Rational constraints: xy + 5y = 3x + 6 becomes xy – 3x = 6 – 5y x(y – 3) = 6 – 5y |
5) 3rd degree Rational
constraints:
|
 |
 |
 |
.
(all content of the MathRoom Lessons © Tammy the Tutor; 2004 - ).