
| VOLUMES OF SOLIDS BY SHELLS |
Definition:
A solid of revolution is the circular solid formed when an area of the plane is revolved around a given line of symmetry or axis.
Cylindrical Shell Method
The easiest way to understand this method is to think of how an onion is constructed. It is a mass of concentric shells, one inside the other, that's why we can make onion rings --yum!
In this approach, we sum the volumes of concentric cylindrical shells, so now, we're decomposing the solid in a direction parallel to the axis of revolution instead of perpendicular to it.
Let's take the area enclosed by y = x 1/ 2, the line x = 4 and the x-axis, and revolve it about the y-axis, creating a circular hole in the center of the solid -- sort of like we punched out the center core of the onion.
Here's the picture of the solid and a cross sectional view:

Each of the shells is a hollow cylinder, so the volume of the solid part is the difference between the volumes of the outer and inner cylinders. The volume of one such shell will be:

Let's mangle this thing a bit to put it into the form we need. First, we'll factor the difference of squares in the bracket, then we'll multiply and divide by 2. Magically, we will produce the formula for the shell method which takes into account the hole in the center of the solid. Here goes.
We have

(R – r) is just the thickness of each shell -- the difference in the outer and inner radius, so we can call it dx, since it is a tiny chunk of the x-axis, which will become zero since the integral limits the number of shells to infinity.
So (R – r) = dx
(R + r)/2 is just the average of the 2 radii and so is the midpoint of the interval defined by the shell's outer and inner walls -- it's just a value of x.
So (R + r)/2 = x.
And h, the height of the shell is just the y-value paired with that midpoint x-value.
So h = y = f (x)
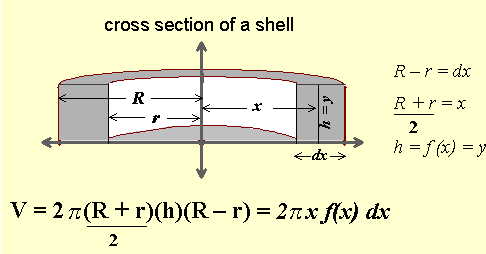
Because of all this, the shell method formula for finding the volume of a solid of revolution is:

So in the example above, we get 
IMPORTANT: Notice that though we revolved about the y-axis, we integrated with
respect to x.
With the shell approach, we integrate with respect to the axis the shells stand on.
If they don't make it to the axis -- they're cut off by another function's curve, then the height of each shell is no longer f (x) -- it's now f (x) – g (x). For instance, had we revolved the area between y = x² and y = x 1/ 2 about the y-axis, the solid would look like this and each shell's height would be ( x 1/ 2 – x² ) instead of just x 1/ 2.

Which Method is Best?
As mentioned in the lesson on Disk Method, there are questions where we have no choice but to use Shell Method because it doesn't work on the given situation. The image will make it obvious.
We'll revolve about the y-axis, the area between y = 4x – x² and the x-axis.

In such a case, we decompose the solid parallel to the axis of revolution so we use Shells.


.
Sometimes, the solid formed is split symmetrically by an axis, so we find the volume of half of it, then double it, as in this example. This is true for both methods of finding the volume of solids of revolution.
Example: Use shell method to find the volume of the solid formed by revolving about the x-axis the area between the curve y = x 1 / 2 and the line x = 4.
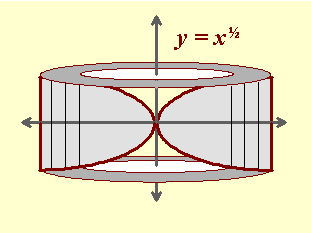
It's pretty obvious that the volume of the top half of the solid (above the x-axis) is identical to the volume of the bottom half. So we find the volume of the upper half and double it to complete the question like this:

.
Summary of Shell Method to find Volume of a Solid of Revolution
Shell Method:
If we revolve about the x-axis:

If we revolve about the y-axis:

**NOTE: Always use the variable corresponding to the axis on which the shells are standing.
If the bottom of the shells are defined by g (x) then:
If we revolve about the x-axis:

If we revolve about the y-axis:

.
Practice
1) Sketch the region bounded by the graphs of these equations and find the
volume of the solid generated by revolving the region about the indicated axis.
| a) y = x 4 , y = 0, x = 1 about x-axis. | b) y = x 3 + 1, x = 0, y = 2 about y-axis |
| c) y = 4x 2,and 4x + y = 0, about x-axis. | d) y = x 3, x = 2, y = 0 about y-axis |
.
Solutions
1)
| a) y = x 4 , y = 0, x = 1 about x-axis.
The shells are not touching the y-axis, and
|
b) y = x 3 + 1, x = 0, y = 2 about y-axis
The shells don't touch the x-axis --
|
| c) y = 4x 2,and 4x + y = 0, about x-axis. The graphs intersect at (0, 0) and ( – 1, 4).
Since we revolve about the x-axis, we integrate with respect to y. We need x = f (y) So, x =½ ( y ½ ) is the top, and x = – ¼ ( y ) is the bottom of the shell.
we factor out ½, multiply the terms to get
|
d) y = x 3, x = 2, y = 0 about y-axis
|
.
( Calculus II MathRoom Index )
(all content © MathRoom Learning Service; 2004 - ).