Definition:

A solid of revolution is the circular solid formed when an area of the plane is revolved around a given line of symmetry or axis.

Disk Method

To find the volume of such a solid using the disk method, we use the fact that every cross sectional slice, cut perpendicular to the axis of revolution, is a cylinder. The volume of the solid is the sum of the volumes of all these cylinders, and, as usual in integral calculus, we limit the thickness of the slice to zero, then sum (or integrate) over the interval indicated.

Let's do an example and then we'll discuss the approach.

We'll take the chunk of y = x ½ from x = 0 to x = 4 and we'll revolve it about the x-axis

The volume therefore is:

.

The previous case was simple since each disk was solid (no hole in the middle). Now let's consider a solid made by revolving the area between y = x² and y = x ^{1/ 2} about the x-axis. These two curves meet at (0, 0) and (1, 1) as shown, causing each slice to be a washer -- a disk with a hole in the middle of it.

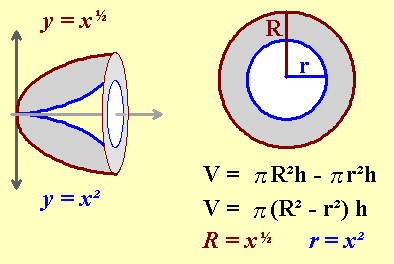
In such a case, the volume is found with

where f (x) is the outer or larger radius, g (x) is the inner or smaller radius, and a, b are the x-values of the points of intersection for the curves.

So in this example,

Note: In all cases so far, we revolved about the x-axis so we integrated with respect to x in all of them. When we revolve about the y-axis, we integrate with respect to y.
If the functions are given as y = f (x), we change them to x = f (y).

.

In certain examples the disk method doesn't work because there's a hole in the middle of the solid, but the outer and inner radii values of the washer slice are x-values in the domain of a single function. Also, as in the example below, we would have to integrate with respect to y because the disks pile up vertically on the y-axis and the inverse of f (x) is difficult or impossible to integrate. In such a case, we have no choice but to use the Shell Method explained in the next lesson. The image will make it obvious.

We'll revolve about the y-axis, the area between y = 4x - x² and the x-axis.

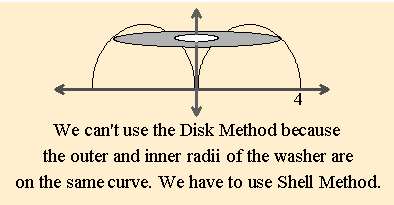
So we'll decompose the solid parallel to the axis of revolution with concentric shells.

If we did want to use the disk method here, we'd have to find x in terms of y and here's what we'd get:

Now we would have to integrate with respect to y and it would be difficult and inefficient. The way to go with this type of question is the Shell Method.

.

One last challenge.

Let's make another solid by revolving about the line x = 2 the area between y = (x – 2)² ,
the line y = 4, from x = 0 to x = 2. Here's what it looks like.

We'll take the square root of both sides and transpose the "2" to find x in terms of y.

.

Summary of Disk Method to find Volume of a Solid of Revolution

Disk Method Use when slices are wafer thin cylinders or discs.

If we revolve about the x-axis:

If we revolve about the y-axis:

Both these equations are just , the formula for the volume of a cylinder, since each disk we cut is a cylinder with radius = f (x) and height or thickness = dx.

.

If there is a hole in the center of the disk, f is the outer radius and g is the inner radius, so:

If we revolve about the x-axis:

If we revolve about the y-axis:

.

Practice

1) Sketch the region bounded by the graphs of these equations and use Disk Method to
find the volume of the solid created by revolving the region about the indicated axis.

a) y = x 4 , y = 0, x = 1 about x-axis.	b) y = x 3 + 1, x = 0, y = 2 about y-axis
c) y = 4x 2,and 4x + y - 8 = 0, about x-axis.	d) y = x 3, x = 2, y = 0 about y-axis

2) Sketch the region bounded by the graph of the parabola y = 4x - x² and the x-axis.
Use Disk Method to find the volume of the solid created by revolving this region
about the line y = 6.

.

Solutions

1)

a) y = x 4 , y = 0, x = 1 about x-axis. We have f (x) = x 4 and this is the radius, so: We get	b) y = x 3 + 1, x = 0, y = 2 about y-axis We need x in terms of y. We get x = (y – 1) 1/ 3 We get
c) y = 4x 2,and 4x + y – 8 = 0, about x-axis. The graphs intersect at (–2, 16) and (1, 4). Outer R = line, Inner r = parabola. We get	d) y = x 3, x = 2, y = 0 about y-axis We need x in terms of y. We get x = y 1/ 3 We get

2)

.

( Calculus II MathRoom Index )

(all content © MathRoom Learning Service; 2004 - ).