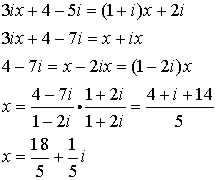
| Complex Numbers and Equations |
Table of Contents
| A/ Definition of Equality |
| B/ Linear Equations with Complex Solutions |
| C/ Quadratic Equations with Complex Solutions |
| Practice |
| Solutions |
.
.
Before we can solve equations with complex solutions, we must define the equality relation between such numbers. We must specify what it means for two complex numbers to be equal. Well, since every complex number is made up of a real and an imaginary part, it seems logical to state that the real parts must be the same and the imaginary parts must be equal to make two complex numbers equal to each other
| Two Complex numbers a + bi and c + di are equal if and only if a = c and b = d. The Real parts a and c are equal and |
.
B/ Linear Equations with Complex Solutions
Using the definition of equality between complex numbers, we can easily solve linear equations in one or two variables as shown in these examples. In the case of two variables, we generally end up solving a system of two equations in two unknowns. For one variable equations, we use the technique of multiplying by the conjugate unit fraction to divide by the coefficient of the variable we seek.
.
Example 1 (2 unknowns)
Find values for x and y if
3x + yi = 5x + 1 + 2i
We will put all the variable terms on the left side and leave a complex number on the right side of the equation. Then we'll solve for x and y.
– 2x + yi = 1 + 2i
so, –2x = 1, and yi = 2i
the solution is x = –½, and y = 2.
.
Example 2 (1 unknown)
Solve for x:
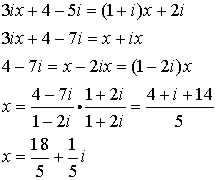
For instructions on dividing one complex number by another, see the previous lesson alg9 on Imaginary and Complex numbers.
.
C/ Quadratic Equations with Complex Solutions
Remember, when we solved quadratic equations with the quadratic formula, there were times that we had to answer "there are no REAL roots or solutions for this equation" because the
discriminant (b² – 4ac) was negative (less than zero). Once we introduce the sets of Imaginary and Complex numbers, every quadratic equation has a solution. Now, we have to state the nature of the solutions as well as the number of solutions. And, as before, when we were restricted to solutions in the set of Real numbers, there are three possiblities. There can be a unique (2 equal) Real or Complex solution, two Real solutions or two Complex or Imaginary solutions. Let's do some examples to illustrate.
Example 3
A unique, Real solution results from the form (x – h)² = 0 with solution x = h.
Solve (x – 5)² = 0. Taking square root of both sides, we get x – 5 = 0, so x = 5.
.
Example 4
A unique, Complex solution results from the form x² + k² = 0 with solution x = k i.
Solve x² + 49 = 0. Transposing 49, we get x² = – 49 so x = 7 i.
.
Example 5
Two Real solutions result from the form (x – h)² = k when k > 0 (k is positive)
Solve (x – 5)² = 25.
Taking root of both sides, we get x – 5 = ! 5,
so x = 5 ! 5 which makes x = 10 or x = 0
If we graph this parabolic function, it will have zeros (x-intercepts) at 0 and at 10.
Example 6
Two Complex solutions result from the form (x – h)² = k when k < 0 (k is negative)
Solve (x – 5)² = – 25.
Taking root of both sides, we get x – 5 = ! 5i,
so x = 5 ! 5i which are conjugates.
x = 5 + 5i or x = 5 – 5i
.
We learned 3 ways to solve Quadratic equations when we were restricted to Real solutions. These methods work for all quadratic equations. They are by factoring, by completing the square and by the quadratic formula. For a lesson on these techniques, study lesson alg6.2 titled Quadratic Equations.
As we can see from the examples above, if we complete the square on the quadratic expression, we can solve easily since we get the form (x – h)² = k, then simply take square root of both sides. The quadratic formula was derived by completing the square on and solving the general form of the quadratic equation ax² + bx + c = 0, so, if we can't factor, we can always use the formula to solve any quadratic equation.
Example 7
Use the quadratic formula to solve x² + 5x + 8 = 0. State the number and nature of the solutions.
In this equation, a = 1, b = 5 and c = 8. Substituting into the formula, we get:

There are two complex conjugate roots.
The discriminant determines the nature of the roots.
If b² – 4ac = 0 there's one Real root.
If b² – 4ac > 0 there's 2 Real roots, and if b² – 4ac < 0 there's 2 Complex roots.
.
1/
a) Determine if 1 + 2i is a solution of x² – 2x + 5 = 0
b) Determine if 1 – i is a solution of x² – 2x + 2 = 0
.
2/ Solve for x and y:
3x + 1 + (y + 2)i = 2x + 2yi.
.
3/ Solve for x. Give answers as Complex numbers.
| a) (3 + i) x + i = 5i | b) (2 + i) x – i = 5 + i | c) (2 + 3i) x – 2i = 2ix + 5 – 4i |
.
4/ Solve these quadratic equations. Give answers as Complex numbers as needed.
| a) x² – 5x + 7 = 0 | b) 2x² – 3x + 2 = 0 | c) – 3x² – 2x – 1 = 0 |
.
.
1/
a) (1 + 2i)² – 2(1 + 2i) + 5 = 1 + 4i + 4i² – 2 – 4i + 5
when we collect like terms, we get : 4 + 4i² = 0.
So (1 + 2i) is a solution of x² – 2x + 5 = 0.
b) (1 – i)² – 2(1 – i) + 2 = 1 – 2i + i² – 2 + 2i + 2
when we collect like terms, we get : 1 + i² = 0, since i² = – 1.
So (1 – i) is a solution of x² – 2x + 2 = 0.
.
2/ Solve for x and y:
3x + 1 + (y + 2)i = 2x + 2yi.
3x + 1 + yi + 2i = 2x + 2yi
x – yi = – 1 – 2i which means x = –1 and y = 2
.
3/ Solve for x. Give answers as Complex numbers.
| a) (3 + i) x + i = 5i (3 + i) x = 4i |
b) (2 + i) x – i = 5 + i (2 + i) x = 5 + 2i |
c) (2 + 3i) x – 2i = 2ix + 5 – 4i 2x + 3ix – 2ix = 5 – 4i + 2i
|
.
4/ Using the quadratic formula, we get
a) x² – 5x + 7 = 0

b) 2x² – 3x + 2 = 0

c) – 3x² – 2x – 1 = 0

.
Back to Algebra MathRoom Index
.