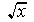 , the square root of x.
, the square root of x.
| rational exponents and radicals |
Rational Exponents and Radicals
Rational numbers are fractions. Notice the first 5 letters in rational, you'll understand.
Let's investigate what x ½ might mean.
If we multiply x ½ by itself, according to the rules of exponents, we get
x ½ $ x ½ = x ( ½ + ½ ) = x 1
By definition, this is the role of a square root: square it -- you get the number.
So, since squaring x ½ gives us x , x ½ must be the same as 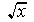 , the square root of x.
, the square root of x.
Similarly, (x 1/ 3) 3 = x so x 1/ 3 must be the same as 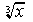
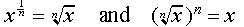
Now consider what x 2/3 means:
x 2/3 = (x 1/ 3) 2 which means 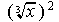
So ( 8 2/3) = (8 1/ 3) 2 = (2) 2 = 4
.
EXTRACTING ROOTS
If the real number under the radical is prime, nothing can be changed.
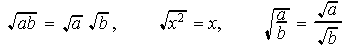
If however, the number under the radical has perfect square factors, extract their roots.
Then, if there are common radicals, combine them.
examples:
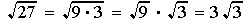 , and
, and 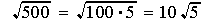
9 is a perfect square, extract its root, 3, to get 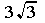 . Same for 100.
. Same for 100.
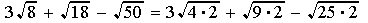
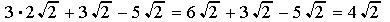
To deal with radicals, factor, extract the square root of any perfect squares,
combine like radicals.
combining radicals is exactly like
combining like terms in algebraic expressions.
(with emphasis on the word LIKE!)
You can't add x and y so you can't add 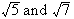 since both 5 and 7 are prime numbers and have no perfect square factors. So nothing can be extracted from the radicals.
since both 5 and 7 are prime numbers and have no perfect square factors. So nothing can be extracted from the radicals.
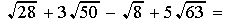
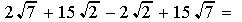
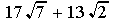
.
COMBINING RADICALS
Combining radicals is a lot like adding or subtracting fractions in that the terms must have something in common. For fractions, the common item is the denominator.
With radicals, we must find a common root, like this:
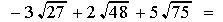
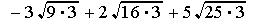
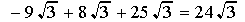
Here, the common element in the three radicals is the square root of 3. Once we have factored the expression(s) under the root and extracted the square root(s) of any perfect square(s), we can combine the like radicals the same way we combine like terms in an algebraic expression.
.
Some examples combining radicals.

|

|

|

|
.
RATIONALIZING
Some radicals such as the square root of 2 are irrational numbers. Long ago, when calculating math questions, we used a slide rule: a device, like the abacus, which was a precursor of today's calculators, but much more primitive and sorely limited. The poor thing was unable to divide by a radical, so, we created a technique called rationalizing, wherein we multiply an irrational root by itself to turn it into a rational number.
When we multiply the square root of 2 by itself, we get the rational number 2.
This is what allows us to rationalize radicals.
since 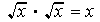
then 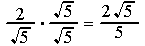
Now the denominator is 5 instead of 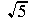 , so the slide rule could divide.
, so the slide rule could divide.
You may wonder why, in the days of calculators and computers, we still bother to teach this technique. There are certain questions on Calculus limits which can only be solved using rationalizing -- and sometimes, you rationalize a numerator instead of a denominator.
Note: to rationalize a fraction with a radical denominator, multiply it by a fraction = 1; composed of the same radical in both its numerator and denominator. Since we mustn't change the value of the given expression, we can only change its form, the fraction by which we multiply must be equal to 1.
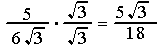
Note: Notice we did not concern ourselves with the 6 in the denominator. Since 6 is a rational number, it need not be rationalized. It is the root of 3 which needs to be rationalized. Just as, when we combine fractions, we use the lowest common denominator, here we use the lowest common radical.
Note: If the radical to be rationalized has perfect square factors, extract their roots, reduce the fractions if possible before rationalizing.
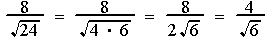
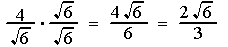
RATIONALIZING BINOMIALS
How do we rationalize a binomial denominator?
Since the product of (a – b)(a + b) = a 2 – b 2
and
the square of any radical is rational
multiply the binomial by its conjugate -- (the same terms with the opposite sign.)
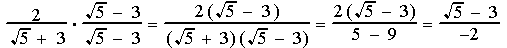
Had the denominator been 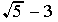 , we would have multiplied by
, we would have multiplied by 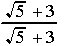 .
.
Here are a few more examples:
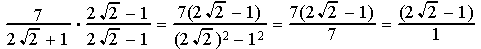
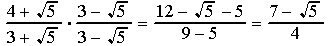
Notice that the numerator after rationalizing is a trinomial,
since it is the product of the 2 binomials 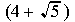 and
and 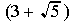 .
.
Now get a pencil, an eraser and a note book, copy the questions,
do the practice exercise(s), then check your work with the solutions.
If you get stuck, review the examples in the lesson, then try again.
![]()
.
PRACTICE:
1/ Simplify and Combine like radicals:
 |
 |
 |
 |
2/ Multiply or Divide as indicated
a) 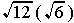 ...... b)
...... b) 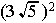 ......c)
......c) 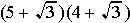
d) 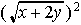 ......e)
......e) 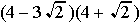 ...... f)
...... f) 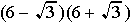
g) 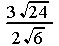 ...... h)
...... h) 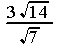 ...... i)
...... i) 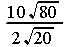 ...... j)
...... j)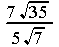
3: Rationalize these denominators
a) 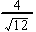 ......b)
......b) 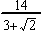 ......c)
......c) 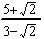 ......d)
......d)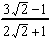
![]()
Solutions
1/ Simplify and Combine like radicals
 |
 |
 |
 |
2/ Multiply or Divide as indicated
a)  |
b)  |
c)  |
| d) x + 2y | e)  |
f) difference of squares so 36 – 3 = 33 |
g)  |
h)  |
i)  |
.j) |
3/ Rationalize these denominators
a)  |
b)  |
c)  |
d)  |
.
(all content © MathRoom Learning Service; 2004 - ).